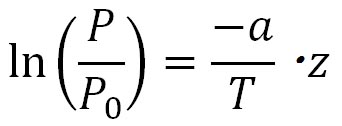対流雲の雲底高度
未飽和の空気塊が上昇すると、その空気塊の温度は乾燥断熱線に沿って低下し、やがて水蒸気が凝結し始め、雲が発生する。その高度は持ち上げ凝結高度（lifting condensation level(LCL))と呼ばれ、この高度は対流性の雲の雲底高度に相当する。この持ち上げ凝結高度については、エマグラムの利用法 (1)ですでに説明した。
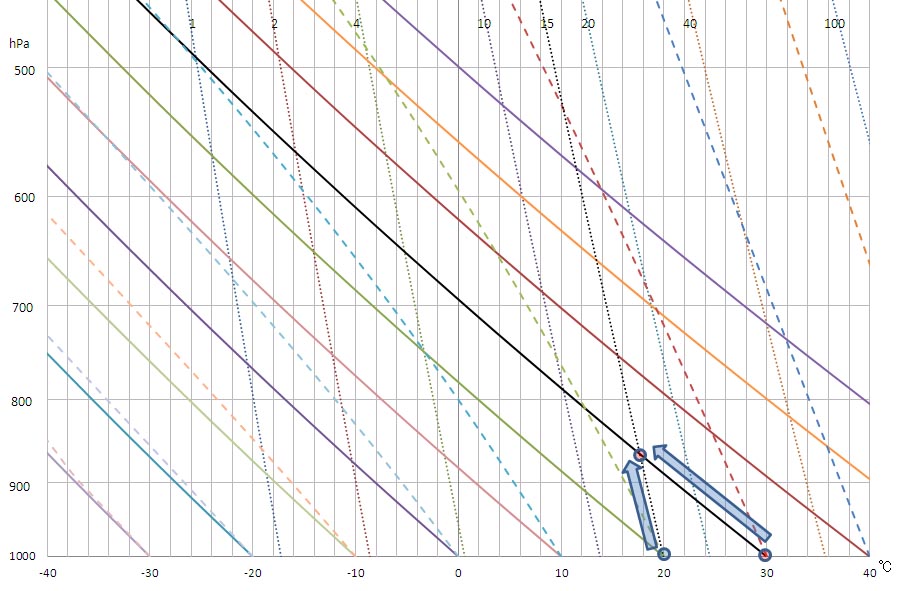
地上の気温と露点温度が分かっていると、エマグラムを利用して、持ち上げ凝結高度を求めることができる。地上の気温が30 ℃、露点温度が20 ℃の場合の持ち上げ凝結高度をエマグラムを用いて求める様子を以下の図に示した。1000 hPaで30 ℃を通過する乾燥断熱線と、1000 hPaで20 ℃をほぼ通過する15 g/kgの等飽和混合比線を上にたどり、その交点の気圧が持ち上げ凝結高度となる。
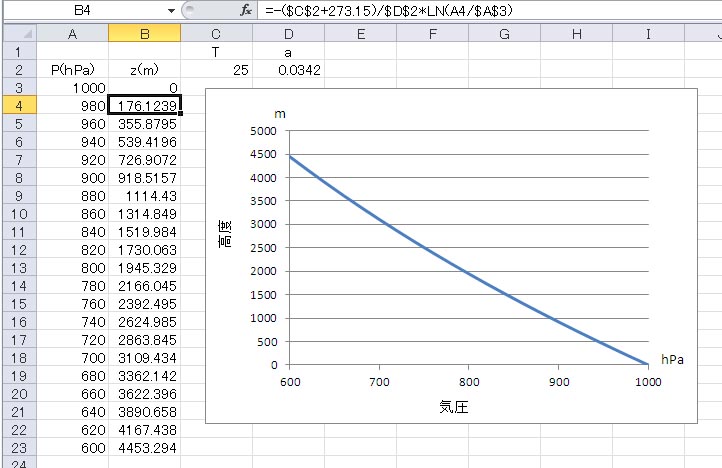
エクセルのグラフでは、片対数グラフの補助目盛線を細かくできないため、グラフから正確な高度を読み取るのは難しい。ただ、グラフの上でおおよその値を読み取った上で、グラフの元となる計算結果の表に、その近くの高度を代入して計算することで、かなり細かく数値を読み取ることができる。上のグラフからは、持ち上げ凝結高度は860 hPaから870 hPaの間にあるようだ。
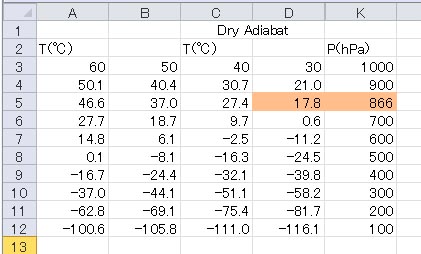
乾燥断熱線を計算する表で、若干の試行錯誤を繰り返した後に、高度に866 hPaの値を代入して計算した結果を上に示す。1000 hPaで30 ℃の乾燥断熱線は、866 hPaでは17.8 ℃になることが示されている。
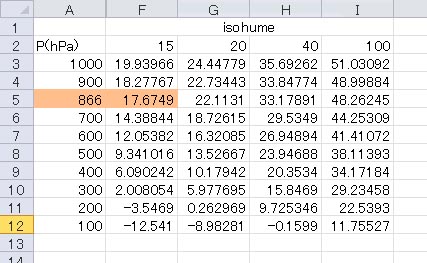
同じく、等飽和混合比線を計算する表で、高度に866 hPaの値を代入して計算した結果を上に示す。1000 hPaで19.9 ℃を通過する15 g/kgの乾燥断熱線は、866 hPaでは17.67 ℃を通過し、866 hPaの高度で乾燥断熱線とほぼ交わっている。以上の結果から、この場合の持ち上げ凝結高度は、ほぼ866 hPaであることが分かる。
それでは、気圧で示された866 hPaの高度とは、距離高度でどのくらいであろうか？気圧と高度との関係式は、片対数グラフを描くで以下の近似式を示した。
ここで、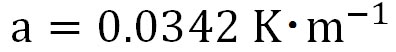 であり、温度は絶対温度で計算する。この式を用いて、気温を25 ℃として計算した結果を下に示す。
例題としてエマグラムで求めた持ち上げ凝結高度の866 hPaに近い値として、上の計算結果の表に860 hPaで約1314 mという値がある。この表の列Aの値は、任意に代入できるので、866 hPaの高度も容易に計算できる。その結果を以下に示す。
 |
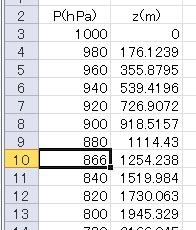得られた結果は1254 mであり、860 hPaの値より60 m低くなった。
ところで、アーレンの教科書には、地上の気温と露点温度の値から、簡便に持ち上げ凝結高度を求める方法が紹介されている。その方法は、乾燥断熱減率線と等飽和混合比線の傾きが一定であるとして計算するものである。
乾燥断熱減率は、(乾燥断熱線図を描く（１））で導いたように、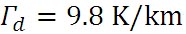 である。これを1000 mで10 ℃低下すると近似する。
アーレンによれば、等飽和混合比線は1000 mで 2 ℃低下しているという。すると、1000 m上昇すると、気温と露点温度の差は10-2=8 ℃縮まる。すなわち125 m上昇すると、気温と露点温度の差が1 ℃縮まることになる。したがって、次の式が得られる。
持ち上げ凝結高度=125×（気温－露点温度）m
ここでエマグラムを用いて求めた例題では、気温と露点温度との差が10 ℃であったので、この式を用いると持ち上げ凝結高度は1250 mとなるが、上で求めた1254 mとほぼ一致している。
実際には、混合比が小さいと、低下割合はこれより小さいし、混合比が大きいと、低下割合はこれよりずっと大きい。実際、混合比が100 g/kgでは、1000 hPaから500 hPaの間で約13 ℃低下しており、混合比が10 g/kgでは、1000 hPaから500 hPaの間で約10 ℃低下しており、混合比が1 g/kgでは、1000 hPaから500 hPaの間で約8 ℃の低下である。地上から3000 mの範囲で、1000 mで 2 ℃の低下となる混合比を調べてみると40 g/kg前後のようである。このことから対流雲の発生しやすい、気温の高い範囲で近似精度が高い式となるようだ。
地上の気温が同じであっても、湿度（露点温度）が高い場所では、対流性の雲の雲底高度は低い。一方、湿度が低い場所では雲底高度が高くなる。アーレンのテキストによれば、夏場の乾燥地帯では気温と露点温度が22 ℃も離れることが普通だが、その場合雲底高度は2750 mも高くなるが、このような場所では高気圧による下降流が発生するため、そこまで上昇気流が届かず、対流雲が発生せずに終わる。
(2011.4.25)
| 
