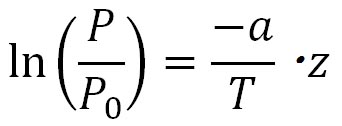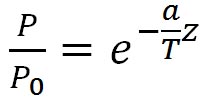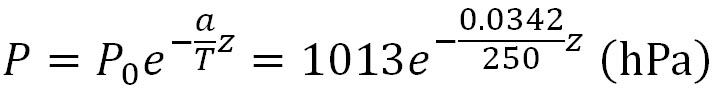|
片対数グラフを描く
指数関数や対数関数が含まれるグラフは、直線座標の上に描くと曲線となるが、片対数座標の上に描くと直線で表され、その関係が明瞭となる。ところで、指数関数と対数関数とは逆関数の関係にある。すなわち、xの指数関数は次のようにに表される。
xの対数関数は次のようにに表される。
xの指数関数の両辺の対数を取ると、
となる。以上の式の関係から、指数関数と対数関数とは逆関数の関係にあることが分かる。ここで、
である。
ここで、
であり、式を変形して定数を代入すると、
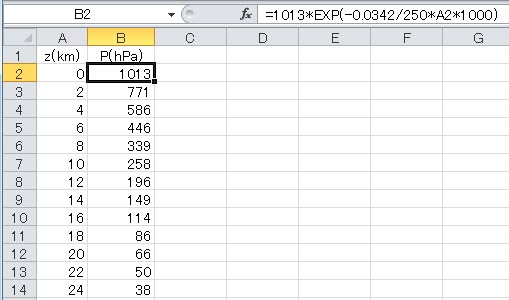
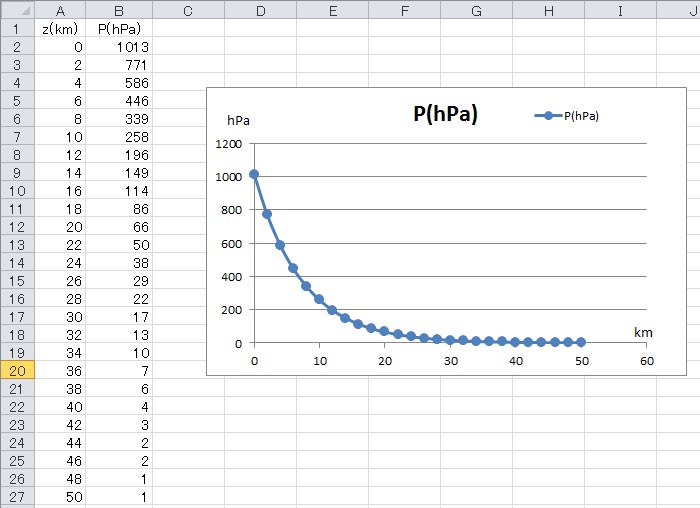
となる。これをエクセルで数値計算する。まず、A1セルに説明変数の表題を、B1セルに目的変数の表題を書き込む。次に、A列にkm単位の高度を、2kmごとにオートフィル機能を用いて書き入れる。続いて、B2セルに=1013*EXP(-0.0342/250*A2*1000)と書き込み、下にコピーする。
エクセルの、自然対数の底eを底とする数値のべき乗を計算する指数関数はEXP()である。A2*1000としているのは、定数aの単位がmであるのに、説明変数zの単位をkmとしたからである。
描かれたグラフは、いわゆる指数関数的に0に漸近して減少するグラフである。このグラフは、途中で大きく湾曲している。
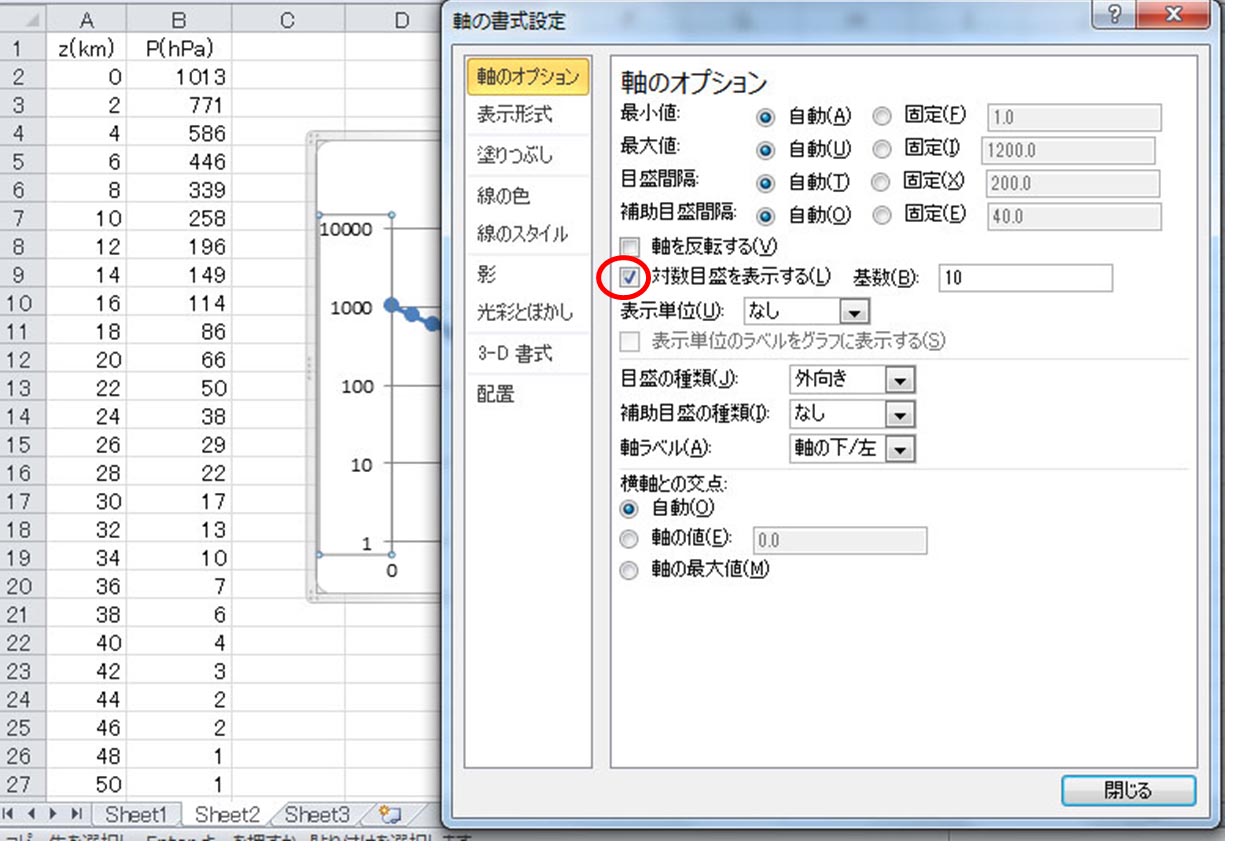
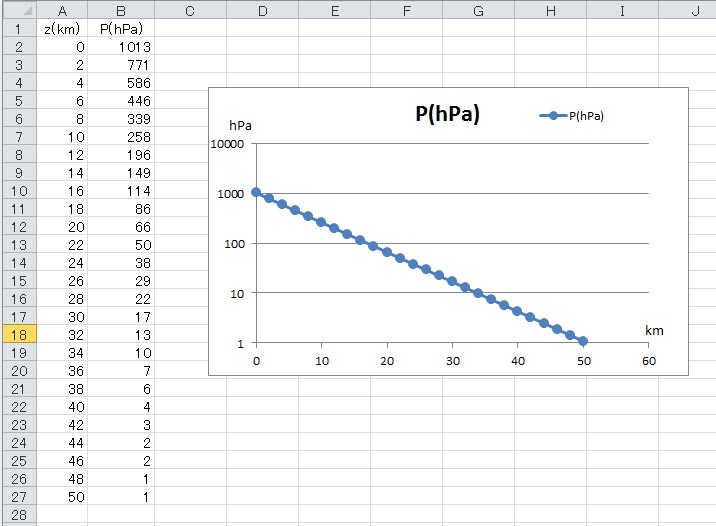
すると、これまで湾曲していたグラフは、瞬時に以下に示すような直線のグラフに変化する。
指数関数のグラフは、片対数グラフでは直線となる。 | ||||||||||||