|
|
サイン関数のグラフをコサイン関数のグラフにする
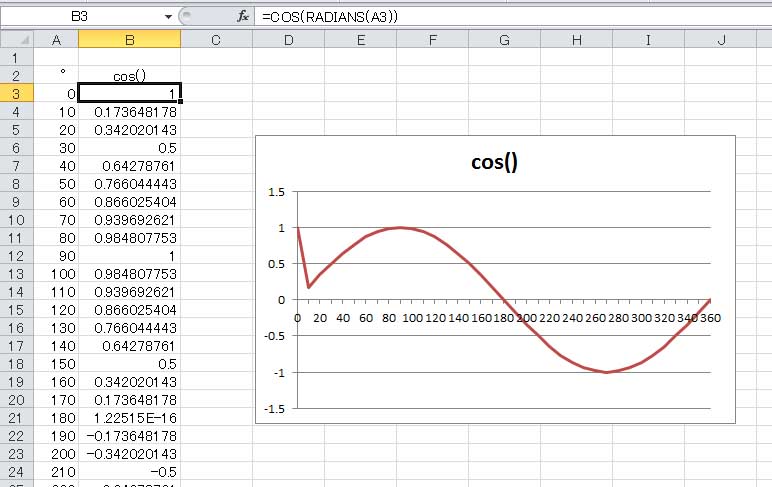
前回までで、一波長分のサイン関数のグラフが一応完成した。このグラフの含まれるファイルを名前を付けて保存で別の名前で保存し、手を加えることによって簡単にコサイン関数のグラフを描くことができる。
上の図は、前回までに作ったサイン関数のグラフの引数の表を 0 °からに変更し、B2セルの sin() という表題を cos() に変え、 B3 セルの数式を SIN(RADIANS(A3)) であったものを COS(RADIANS(A3)) に変更した直後の状態である。 0 °から20 °の間で不連続な曲線となっているが、この部分でコサイン関数とサイン関数とが混在しているからである。
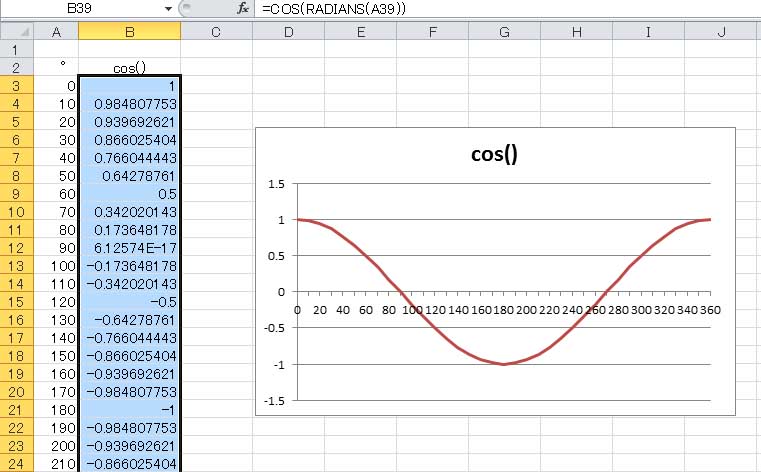
ここで、B3セルの数式をB39セル(360 °)まで下にコピーすれば、1波長分のコサイン関数のグラフが完成する。
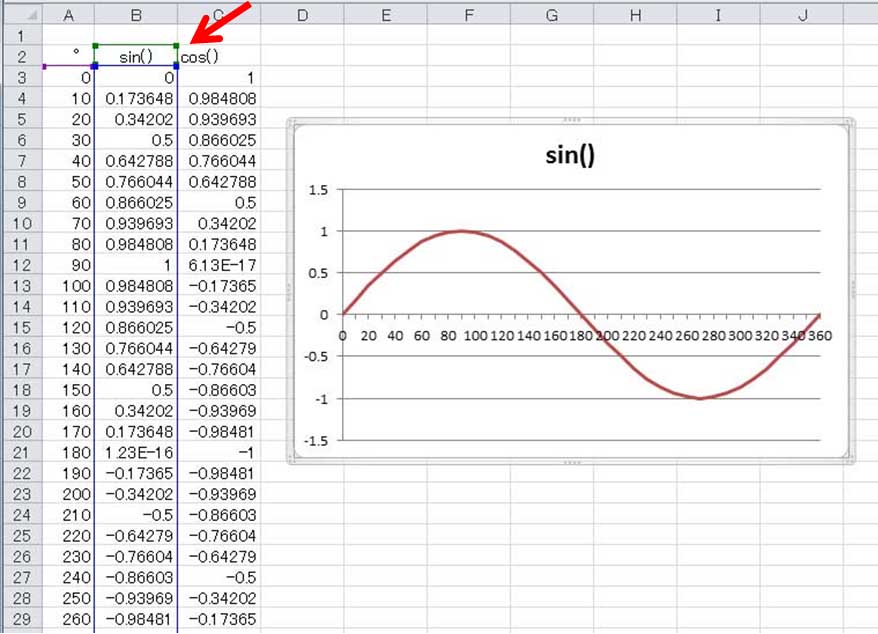
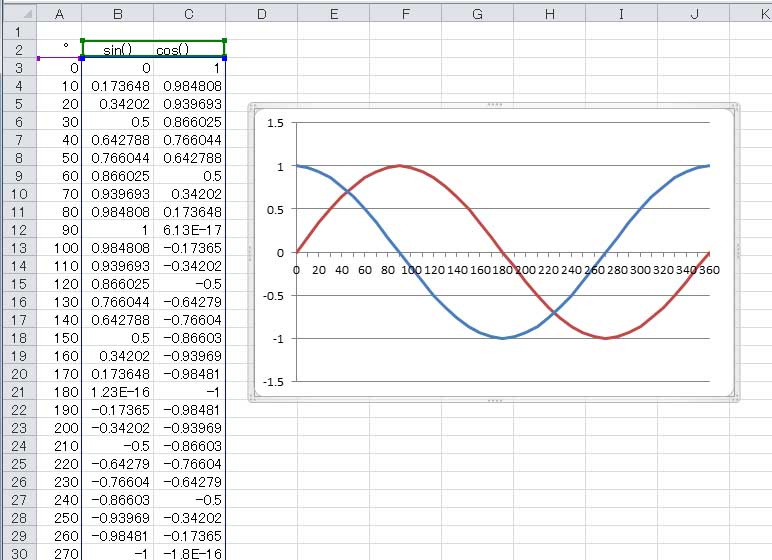
上の図は、前回までに作ったサイン関数のグラフの引数の表の先頭を 0 °に変更した後、 C2セルに cos() の表題を書き、C3セルに COS(RADIANS(A3)) と書き込み、それをC39セル(360 °まで下にコピーしたものである。グラフの上でマウスクリックすると、データの選択範囲を示す青い長方形が現れる。その四隅には、ハンドラーの青い小さい正方形があり、それをマウスでドラッグするとデータの選択範囲を変更できる。
凡例を消去してしまったので、分かり難くなっているが、赤い曲線がサイン関数、青い曲線がコサイン関数である。 | |||||