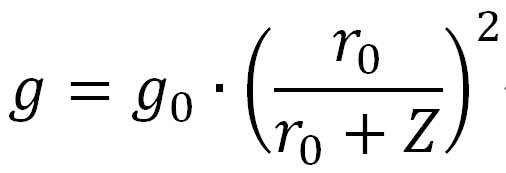重力加速度の高度による変化
重力加速度は、ニュートンの万有引力の法則に基づき、地球と地球上の物体との間に働く万有引力と、その地点における地球の自転に伴って発生する遠心力との合力に基づいて作用する。標準大気モデルの計算だけでなく、大気現象を解析する上では、この重力加速度は重要な役割を果たしている。
地球の海面上の重力加速度の標準値として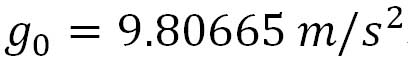 が採用されたのは、1901年の国際度量衡総会であった。この値は緯度45 °における海面の重力加速度の値とされたが、その後、この値は約0.05 %大きいことが分かった。現在では、緯度45 °32 '33 "=45.5425 °での、海面における重力加速度がこの値に近いとされている。 が採用されたのは、1901年の国際度量衡総会であった。この値は緯度45 °における海面の重力加速度の値とされたが、その後、この値は約0.05 %大きいことが分かった。現在では、緯度45 °32 '33 "=45.5425 °での、海面における重力加速度がこの値に近いとされている。
二つの物体に働く万有引力の大きさがその物体間の距離の2乗に反比例するという法則から、地球上の任意の高度における重力加速度gの大きさは、
で精度よく近似できる。ここで、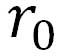 は、注目している点での地球の半径で、これはその地点での遠心力の大きさに関係する。ただ、簡単のため、その地点の地球の半径を、地球半径の平均値である は、注目している点での地球の半径で、これはその地点での遠心力の大きさに関係する。ただ、簡単のため、その地点の地球の半径を、地球半径の平均値である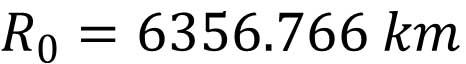 として計算しても誤差が小さいとして、1976年の米国標準大気モデルでは として計算しても誤差が小さいとして、1976年の米国標準大気モデルでは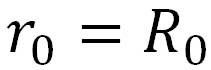 として計算している。 として計算している。
ここで、この式にしたがって、地球上の重力加速度が高度によってどのように変化するかをグラフにしてみよう。
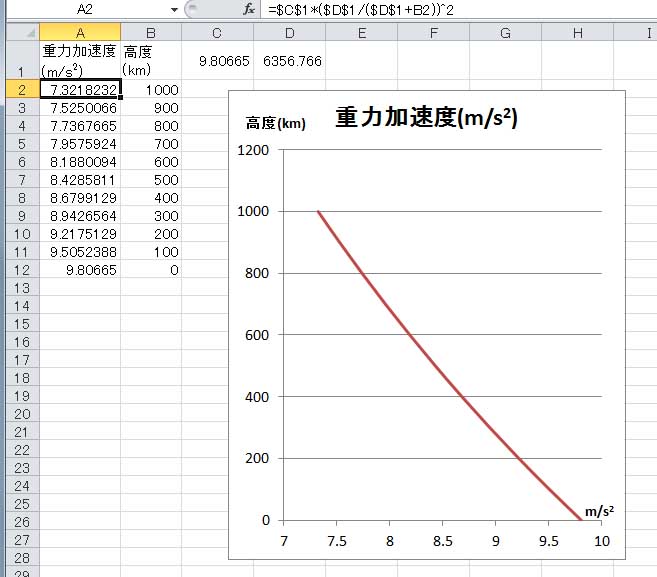
上の図が完成したグラフである。地上の高度が説明変数で、重力加速度が目的変数だが、目的変数を縦軸方向に表したいので、高度を2列目に、重力加速度を1列目とする。それぞれ1行目に表題を書き込んだ。
B2セルに1000 と、B3セルに900と書き込み、B12セルまで自動挿入して、縦軸を作成した。C1セルに重力加速度の標準値9.80665を書き込み、D1セルに地球半径の平均値6356.766を書き込んだ。そして、A2セルに、関係式である=$C$1*($D$1/($D$1+B2))^2を書き込んでA12セルまで下にコピーした。書式を若干整えたグラフが上に示したものである。
上のグラフを見ると、若干湾曲しているが、ほぼ直線的に重力加速度が減少しているように見える。
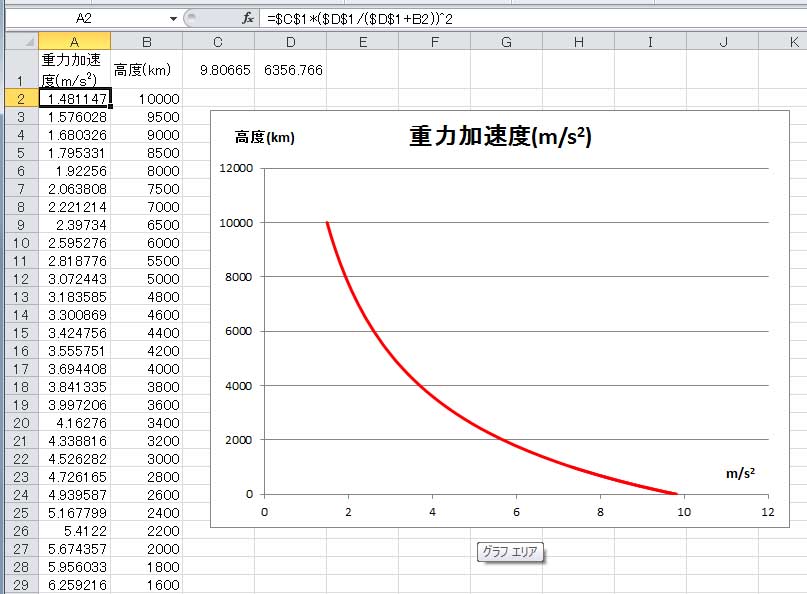
続いて、1行目と2行目との間に30行ほど行を挿入し、縦軸目盛を10000 kmまで延長し、A列に関係式をコピーして描いたグラフを下に示す。
高度がさらに増加すると、重力加速度の減少割合が鈍っていき、グラフが大きく湾曲してくることが分かる。
|