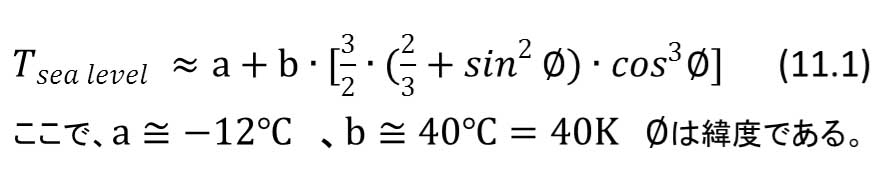ここまでの要領が分かれば、気象学で扱う三角関数が含まれた少し複雑な式のグラフも描けるものが出てくる。例題として、地球の各緯度による平均気温の分布図を描いてみよう。使用する式は、ローランド・シュトゥールの教科書(*)の11.1式である。地球上の各緯度の年間平均の海面補正気温を示す関数である。

　この関係式は簡略化されたモデルに基づく式であり、玩具のようなモデルということで、シュトゥールはトイ・モデルの例として挙げている。それでも、数式になじみのないものには複雑な式に見えるかもしれない。

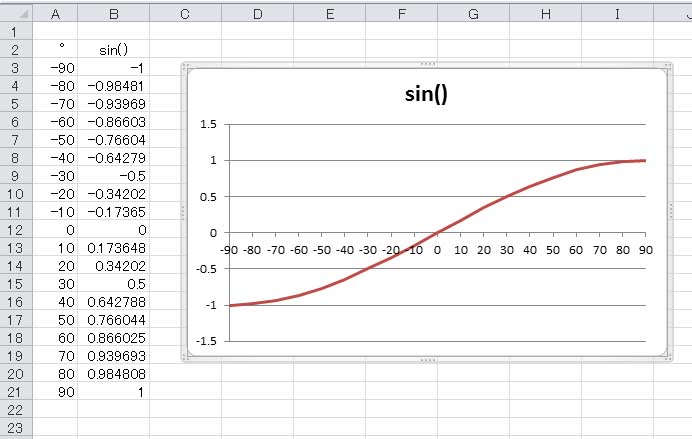
　緯度の値を、赤道で0 °、北極で90 °、南極は-90 °とすると、この講座で最初に描いたサイン関数の引数の表が利用できる。ということは、その時の結果のファイルに手を加えることで、この関数のグラフは簡単に描くことができる。

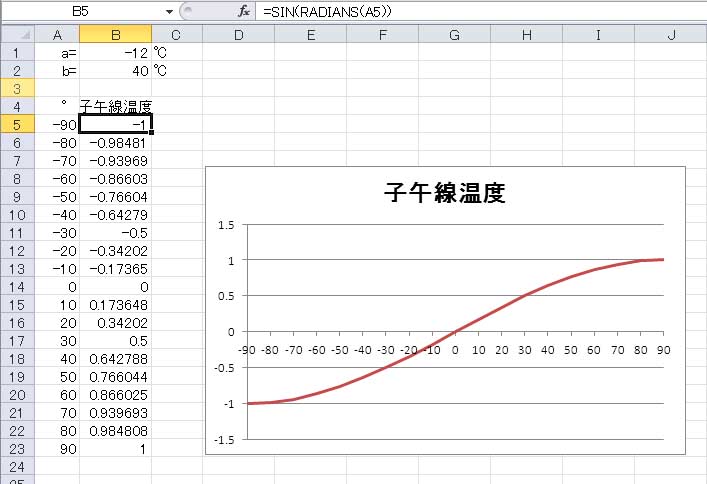
　上の図が、その時描いた-90 °から90 °までの半周期分のサイン関数のグラフであるが、最初に若干の手を加える。

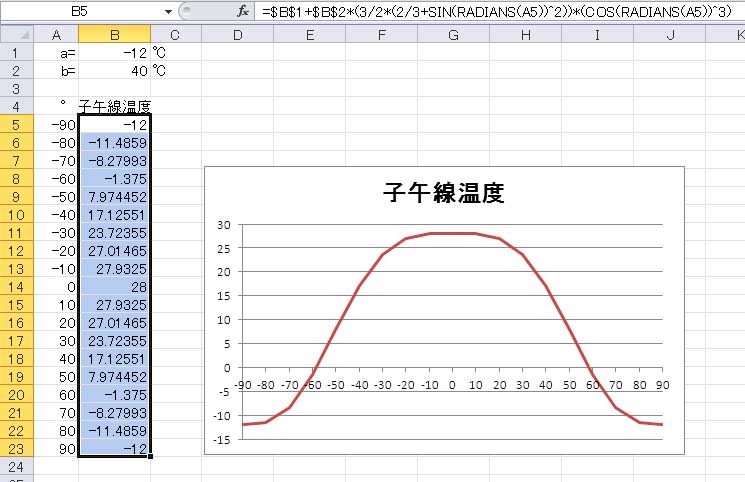
　上に示したように、先頭に2 行足して定数 a と b の値を入れるセルの設定を行い、表題をsin() から子午線温度に変更した。定数を式の中に書かないことで、一旦グラフを描いた後に、定数を変化させて様子を見ることが容易となる。

　続いて、B5セルに書き込んである=sin(RADIANS(A5) というサイン関数の計算式を=$B$1+$B$2*(3/2*(2/3+SIN(RADIANS(A5))^2))*(COS(RADIANS(A5))^3) に変更する。そして、B5セルを選択して、B23セルまでドラッグして、この式を下にコピーする。

　すると、目的のグラフが瞬時に描かれる。

　ここで、$B$1 はセルB1 の固定参照を示し、下にコピーしても参照セルが下に移動しない。$B$2 も同様にセルB2 の固定参照である。

　^ は、エクセルのべき乗演算子で^2 で2乗を、^3 で3乗の計算を行う。

　計算結果のグラフを見ると、海面温度は両極で-12 ℃、赤道で28 ℃で、中緯度域で傾斜が急な山型の温度分布となっている。