三角関数とは、基本的には直角三角形の辺の長さの関係を表す関係式であり、振動や円運動の解析には欠かせない。慣れないと難しく思われるが、慣れてしまえば大変便利な関数である。

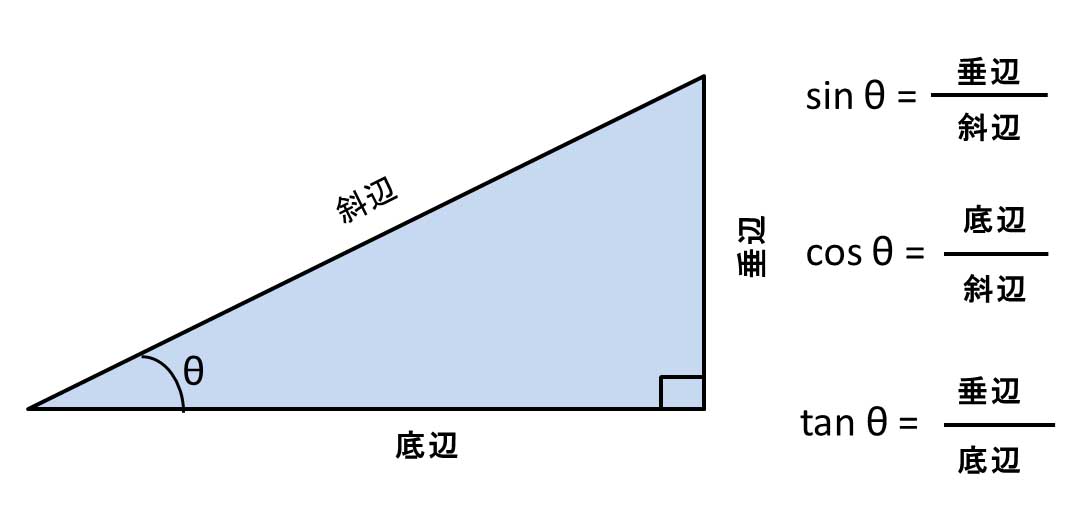
　直角三角形の各辺を、下図に示すように、斜辺、底辺、垂辺とし、直角三角形の底辺と斜辺との間の角度をθとすると、sinθ（サイン角シーター）は、（垂辺／斜辺）、cosθ（コサイン角θ）は（底辺／斜辺）、tanθ(タンジェント角θ)は（垂辺／底辺）となる。

　

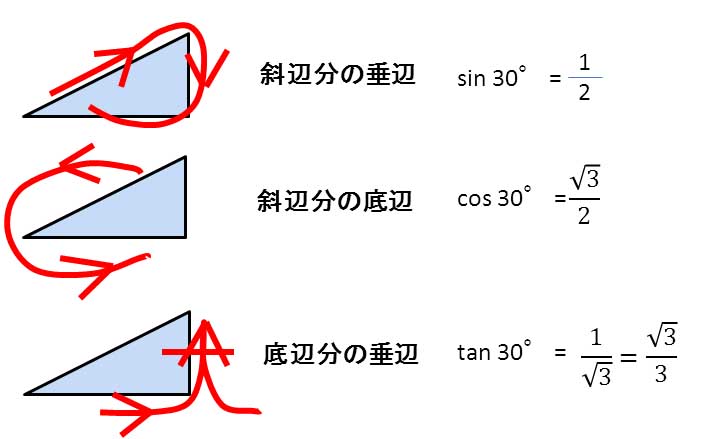
　昔から使われている三角関数の関係式の覚え方として、下図に示すものがある。それぞれの関数の頭文字を使って、サインの s 、コサインの c 及びタンジェントの t の小文字筆記体の書き順で覚える。すなわち、サインは斜辺分の垂辺、コサインは斜辺分の底辺、タンジェントは底辺分の垂辺と覚えるのである。

　それぞれの関数値の代表例として、θが30度（30π／180＝0.5236ラジアン）のときの値も以下の図に示す。

　角度の表し方には60分法と弧度法とがあり、度数単位で表現する60分法をラジアン単位で表現する弧度法に換算するには、60分法の数値に π／180 を掛ける。

　三角法の計算は、以前は数表を引いたり、計算尺を用いたりして行ったものである。簡単な式のうちはよいが、計算式が複雑になると、面倒な作業となる。現在はパソコンの表計算ソフトによって、簡便に計算できるようになっている。以下、代表的な表計算ソフトであるマイクロソフト・エクセルを例にして説明する。

エクセルの関数計算

　エクセルで関数計算をするには、セルに =f(x) の形の式を書き込む。式の先頭に 「＝」 を書くことによって、それ以下の文字が関数を表現しているとエクセルは解釈し、その関数の計算結果がセルに表示される。一例として、 cos(0) (コサイン0ラジアン）の関数を計算した様子を示す。括弧の中にある 0 を関数の引数と呼び、引数が 0 の時の関数の値が計算される。

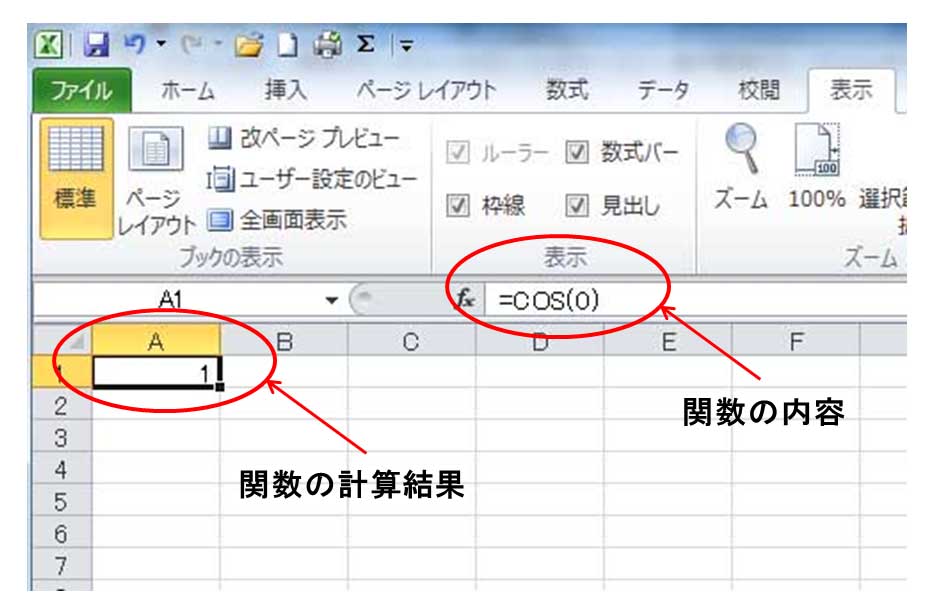　セル（ここではA1）には計算結果が表示され、関数の内容は表示されない。代わりに、上の fx と書かれた右側の枠に関数式が表示されており、関数式を編集する際は、この欄で編集する。

　エクセルの三角関数は弧度法（ラジアン）によっているので、60分法で表した角度を三角関数の引数 (x) に代入する際には π／180 を掛ける必要がある。エクセルでは π を表す式は pi() である。したがって pi()/180 と書き込む。ただし、エクセルには60分法の引数を弧度法に変換する RADIANS() という便利な関数があるので、それを用いた方が文字数は多くなるが間違いはない。30度をラジアンに直すには、RADIANS(30)と書けばよいだけである。

エクセルの三角関数の基本

　エクセルの三角関数のうち、基本となるサイン、コサインとタンジェントについてまず説明する。サイン関数は sin()、コサイン関数は cos()、タンジェント関数は tan()である。サイン30度の計算をするときには、エクセルの任意のセルの中に =sin(RADIANS(30)) と書き込むと、そのセルが 0.5 と表示される。同様にコサイン30度を求めるには、任意のセルに =cos(RADIANS(30)) と書き込むと、そのセルの値が 0.866025403784439 となる。同様にタンジェント30度を求めるには任意のセルに =tan(RADIANS(30)) と書き込めばよい。そのセルは、即座に 0.577350269 と表示される。

　なお、エクセルで用いる関数の名前（綴り）は、エクセルのヘルプにはすべて大文字で記載されている。ただ、小文字で書いた場合には、自動的に大文字に変換されるので、あまり深く気にする必要はない。それよりも、綴りを間違えないことが重要だ。正しくタイプしたつもりになっていても、綴りに誤りがあるとエラーとなってしまう。

　ここで、表示する数値の有効桁数は任意に選べて、有効数字調整ボタンで簡単に調整できる。

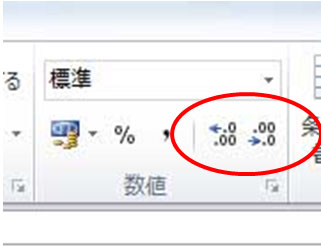　上の図の赤で囲んだ部分にある二つのボタンのうち、左側の ←.0 .00 ボタンを押すたびに有効桁数が一桁増加し、右側にある .00→.0 ボタンを押すたびに有効桁数が一桁減少する。値は、最少桁の次の値を四捨五入した値が示されている。ただし、エクセルの内部の計算式の有効桁数の関係で、少数点以下15桁が最大の有効桁数になっていて、それ以上有効桁を増やしてもその先は0 が追加されるだけである。