|
気圧の高度変化のグラフを描く (2)
前回、近似式を計算して気圧の高度変化のグラフを描いた。そして、高度にかかわらず気温を一定値とした場合と、高度上昇に伴う気温変化を考慮した場合の2種類のグラフを比較した。それでは、ここで計算した2種類の気圧の計算結果のどちらが実際の値に近いのだろうか?もちろん、気圧の値は緯度、経度、季節によって変化するが、ここでは、1976年米国標準大気モデルの値と比較してみよう。
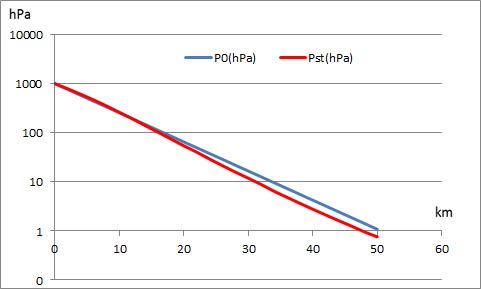
上に示したグラフは、気温を高度にかかわらず250 Kの一定値として計算した大気圧P0を青い線で、1976年米国標準大気モデルの大気圧Pstを赤い線で示してある。このグラフでは分かり難いが、計算値の青い線は、高度10kmまでは赤い線より下にあり、それより高い高度では赤い線より上にある。片対数グラフでは、その差が高度上昇とともに目立つようになる。
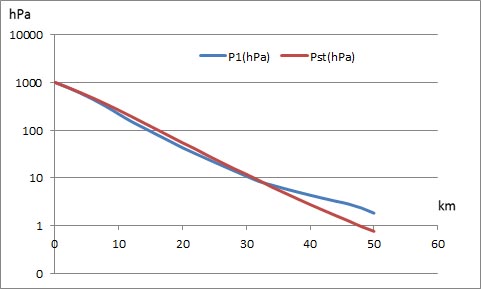
上のグラフは、各高度の気温の値として、1976年米国標準大気モデルの気温を代入して計算した大気圧P1を青い線で、1976年米国標準大気モデルの大気圧Pstを赤い線で示してある。高度32 kmまでは青い線が赤い線の下にあり、それより上の高度では青い線が赤い線の上にある。その差は片対数グラフ上で、高度上昇とともにかなり目立つようになる。
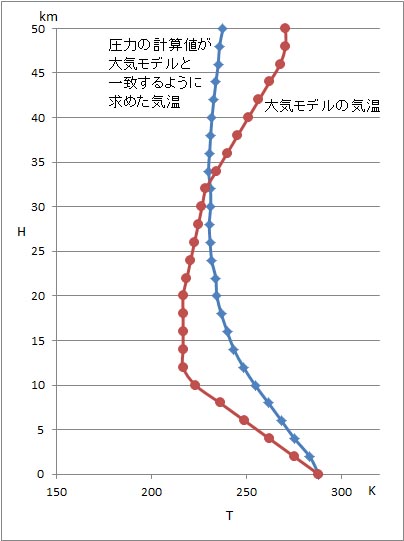
赤色で示した線は、米国の標準大気モデルの気温の高度変化のグラフで、青い線は、大気圧の近似式が、米国の標準モデルの大気圧に一致するように選んだ気温の高度変化のグラフである。このような差が現れるのは、大気圧を単純な指数関数で計算できないことを示している。ただ、単純な式にもかかわらず、十分な精度で近似できているという見方もできる。
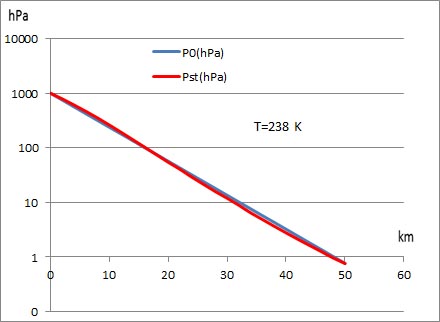
上のグラフは、温度Tを全区間で238 Kの一定値で計算したP0とPstを片対数グラフで示したものである。高度 10 kmまではP0の値がPstより小さく、高度10 kmより上空ではP0の値がPstより大きいという傾向はT=250 Kの時と同じである。 | |||||