|
熱指数のグラフを描く
風速冷却は、寒冷時に強風に当たると体温の低下が著しくなり、凍傷や低体温症に陥る危険性を評価するものである。一方、気温が高い時期に湿度が高いと、湿度が低い時と比較して、汗の蒸発が悪くなり、体表から気化熱が奪われにくくなるため、体感気温は上昇し、不快感が増大する。この不快感を指標化したものとして、以前は不快指数が有名だった。不快指数が８０以上なら全員不快という分かりやすい指標で、昔はラジオやテレビの天気予報で、夏場は不快指数を伝えていたと記憶している。最近の天気予報では、不快指数の言葉を聞くことはほとんどなくなった。
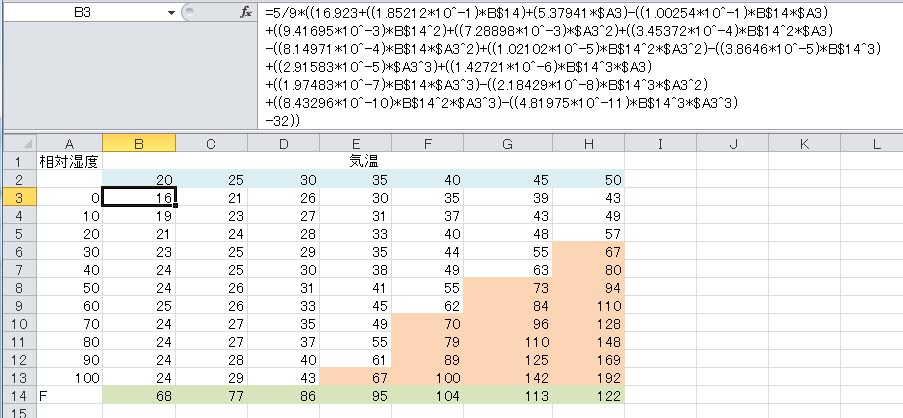
乾湿球温度計があれば、その示度を上の式に代入すれば不快指数は計算できる。しかし、気温と相対湿度が与えられている場合には、この式から不可指数を計算することはできない。一方、気温と相対湿度から、体感気温を計算する熱指数（Heat Index)が各種提案されている。それらは、どれも一長一短があるようで、どれが良いと簡単にいうことはできないらしい。そのような中で、http://www.zunis.org/16element_heat_index_equation.htm に、次のような16項からなる熱指数の計算式が紹介されている。
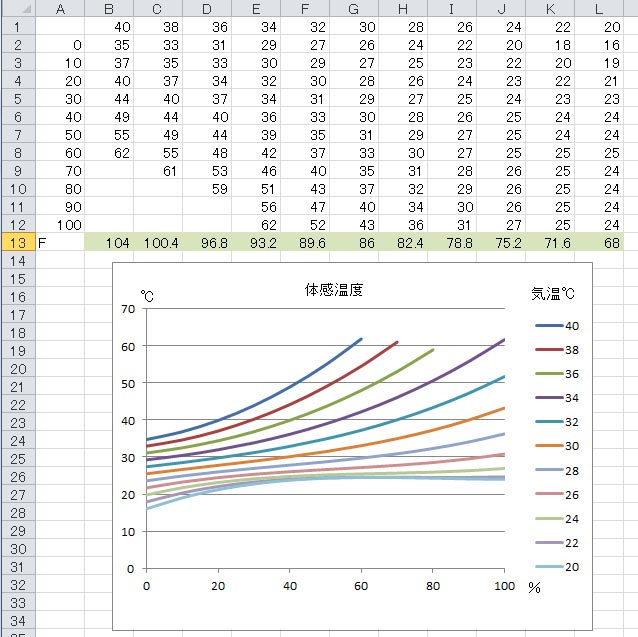
計算式を書き込んで得られた計算結果を上の図に示す。２行目に５℃間隔で摂氏の気温を書き込み、１４行目にそれを華氏に変換した値の計算値を入れた。例えば、B14セルには =B2*9/5+32 と書き込まれている。この関数式を右にコピーすれば、１４行目が完成する。１４行目は参照行で、薄緑色で塗りつぶした。
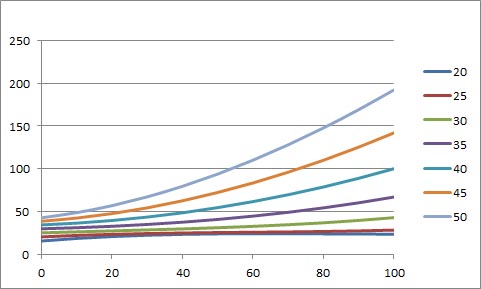
華氏に換算した温度の行を除く部分を選択して、散布図を描いた結果を上に示した。どういう訳か、凡例の並びが、上側ほど低い温度で、下側に向かって高い温度となってしまった。この不都合を除くために、気温の並び方を高い方から低い方へと変更し、散布図を描いたのが下の図である。
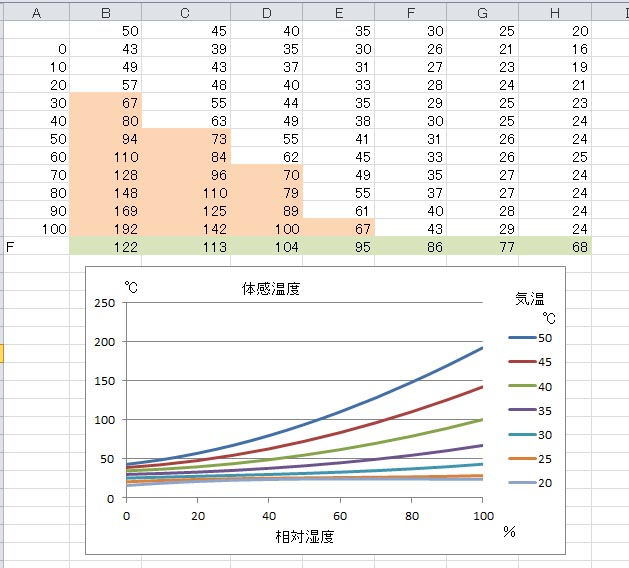
上のグラフを見ると、気温５０℃で相対湿度１００％の時の体感温度は２００℃近くになってしまうことが分かる。ここで紹介した熱指数の適用可能範囲は、華氏７０度以上と指定されているが、あまり高い気温の場合も守備範囲ではなさそうだ。上に示したエクセルの表で、肌色で塗りつぶした部分は、Roland Stullの教科書で空白になっている部分である。不都合な値とみなしたものと考えられる。
そこで、この不都合部分を消去してグラフを描くと、上に示したグラフが得られる。縦軸方向の変化が拡大され、体感温度の変化傾向がずっと見やすくなった。気温が高いと、相対湿度の上昇による体感温度の上昇が激しいことが良くわかる。
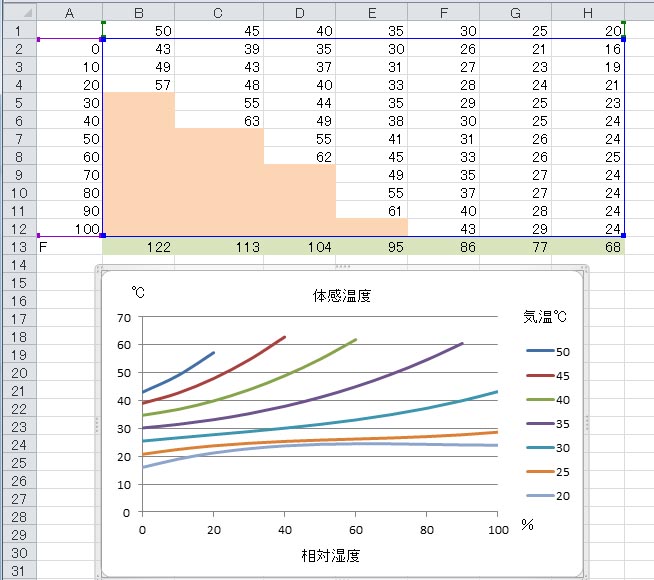
日本では、気温が５０℃になることは考えにくいので、より現実的な範囲として、気温２０℃から４０℃まで２℃間隔で作成したグラフを上に示す。気温２０℃と４０℃では、相対湿度が約２０％以下で体感温度が実際の気温より低く、気温３０度前後では、相対湿度が約４０％以下で体感温度が実際の気温より低くなっている。
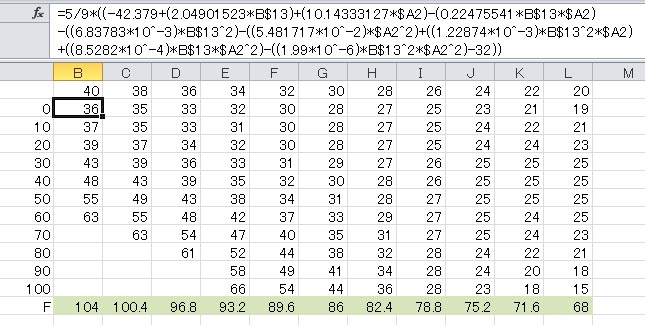
関数ボックス内に、B2セルに書き込んだ関数式が表示されている。この関数式をすべてのセルにコピーすれば完成である。この計算結果においても、摂氏６５度以上と、熱指数が異常に高くなるセルは空白にした。
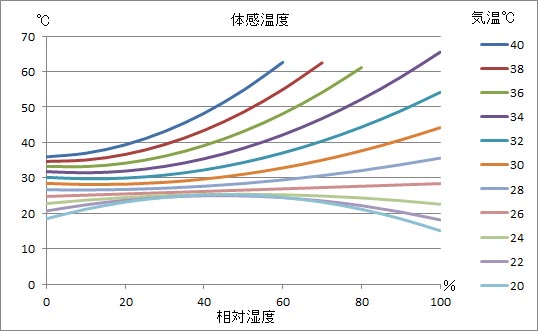
計算結果のグラフを上に示す。気温が２０℃から２４℃のグラフが、相対湿度が５０％以上に増加した場合に、熱指数が低下してしまっている。２６℃のグラフも、相対湿度が高い部分での熱指数が、１６項の結果と比較して少し低い。逆に、相対湿度が低い場合で、９項による計算値は１６項の結果と比較して熱指数が高く計算されている。これらの点を除くと、１６項の式の結果と９項の式の結果は、かなり良好に対応している。 (2010.2.19) | |||||||||
℃、湿球温度を
℃とすると、不快指数(Discomfort Index)DIは以下の式で計算される。
