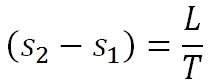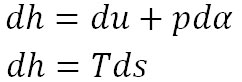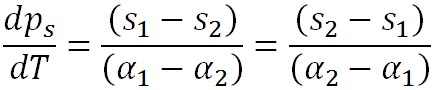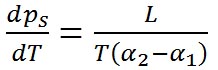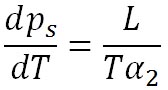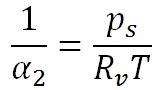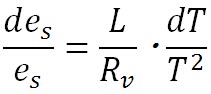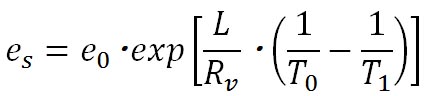飽和水蒸気圧曲線を描く (1)
水面あるいは氷面からは、それと接する空気に向けて、水の分子が絶えず飛び出している。それと同時に、空気中から水面あるいは氷面に向けて、水の分子がやはり飛び込んでいる。水と空気の温度が等しく、飛び出す水分子と飛び込む水分子の数が等しくなっている(平衡状態にある)とき、空気は水蒸気で飽和しているという。そしてこのときの空気中の水蒸気の分圧を飽和水蒸気圧という。
飽和水蒸気圧は温度によって変化する。飽和水蒸気圧の温度による変化の様子を示す理論式に、クラウジウス・クラペイロンの式(Clausius-Clapeyron equation)がある。少し長くなるが、はじめにクラウジウス・クラペイロンの式を導出してみよう。
水には、水蒸気(気相)、水(液相)と氷(固相)の3相がある。これらの相のうちのある相から別の相に移ることを相変化という。相変化する際には、潜熱と呼ばれる熱を吸収したり放出したりする。氷から水へ、水から水蒸気へ、あるいは氷から直接水蒸気へと相変化するときには、水や氷は熱を吸収する。その逆に、水蒸気から水へ、水から氷へ、あるいは水蒸気から直接氷へと相変化するときには、水蒸気や水は熱を放出する。
ここで、水の状態から水蒸気へと相変化する際に吸収する潜熱を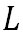 とすると、エネルギーの保存則から、相変化の前後で、以下の式が成り立つ。 とすると、エネルギーの保存則から、相変化の前後で、以下の式が成り立つ。
ここで、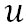 は内部エネルギー、 は内部エネルギー、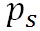 は飽和水蒸気圧、αは比容で、添え字の1は液体の状態の、添え字2は水蒸気の状態の値を示す。この式は、液体の水から水蒸気に変化する際の潜熱は、それぞれの状態の内部エネルギーの差と、相変化に伴う体積の増加によってなされる仕事の和になることを示している。すなわち、相変化に伴うエンタルピーの変化量が潜熱に相当する。 は飽和水蒸気圧、αは比容で、添え字の1は液体の状態の、添え字2は水蒸気の状態の値を示す。この式は、液体の水から水蒸気に変化する際の潜熱は、それぞれの状態の内部エネルギーの差と、相変化に伴う体積の増加によってなされる仕事の和になることを示している。すなわち、相変化に伴うエンタルピーの変化量が潜熱に相当する。
ここで、相変化の間は水と水蒸気の温度は変化しない。したがって潜熱は、相変化時の温度と、水蒸気と液体の状態のそれぞれのエントロピーの差の積となる。すなわち、以下の式が成り立つ。
上の式はエントロピーの定義式でもある。この式は、エントロピーの変化量が、潜熱を絶対温度で除した値であることを意味する以下の形式に変形できる。
エントロピーの単位は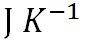 であるが、この式の形から次元が一致していることが分かる。 であるが、この式の形から次元が一致していることが分かる。
潜熱を表す、これら二つの式は等しいことから、これらを等置した次の式が導かれる。
右側の2項を移項して整理すると、以下の式が得られる。
上の式で等値されている左右両辺は、ギブス関数あるいはギブスの自由エネルギーと呼ばれるもので、以下のように表される。
相変化の前後で、ギブスの自由エネルギーが変化しないことを、以下のような式で書くことができる。
ギブスの自由エネルギーの微分は以下のようになる。
ところで、エンタルピーの微分は以下のように表される。
上記の2式の右辺が等しいことから、ギブスの自由エネルギーの微分は以下の式のように整理できる。
ここで、
であることから、
である。この関係式は、以下のように表される。
上の式を、移項して整理すると、
この式をさらに変形すると、
ここで再び、以下の式を思い出す。
この式を用いて、前の式のエントロピーの項を消去すると以下の式が得られる。
ここで、水蒸気の体積は水の体積の1000倍以上あることから、
となり、前の式の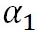 を無視すると、 を無視すると、
が得られる。ここで、水蒸気についても理想気体の状態方程式が適用できると考えると、
が成立する。ここで、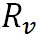 は、水蒸気の気体定数である。この状態方程式を移項して次の形に変形して、二つ前の式に代入する。 は、水蒸気の気体定数である。この状態方程式を移項して次の形に変形して、二つ前の式に代入する。
そして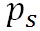 を、飽和水蒸気圧を示す を、飽和水蒸気圧を示す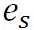 に置き換えると、以下の式が得られる。 に置き換えると、以下の式が得られる。
この変数分離形の微分方程式を解いて得られる式がクラウジウス・クラペイロンの式で、以下のようになる。
この式で、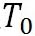 は、水の三重点の温度を絶対温度で表したもので、 は、水の三重点の温度を絶対温度で表したもので、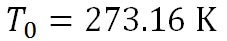 である。 である。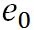 は、水の三重点における飽和水蒸気圧で、 は、水の三重点における飽和水蒸気圧で、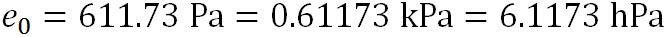 である。 である。
水蒸気の気体定数は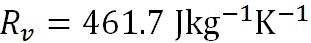 、水から水蒸気へと相変化する際の潜熱 、水から水蒸気へと相変化する際の潜熱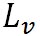 は、 は、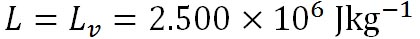 、氷から水蒸気へと相変化する際の潜熱 、氷から水蒸気へと相変化する際の潜熱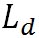 は、 は、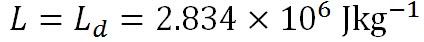 である。以上の値を代入すれば、この式から絶対温度で表した である。以上の値を代入すれば、この式から絶対温度で表した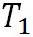 における飽和水蒸気圧が計算できる。 における飽和水蒸気圧が計算できる。
|