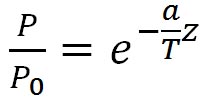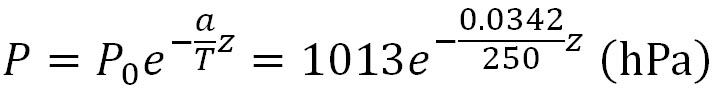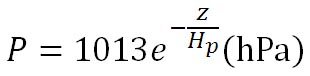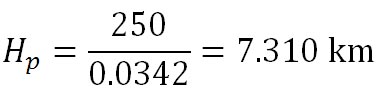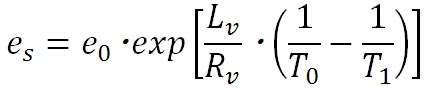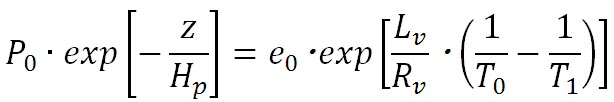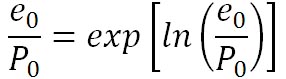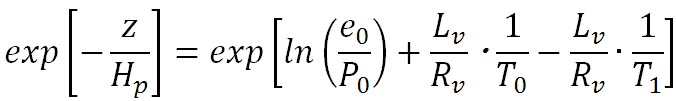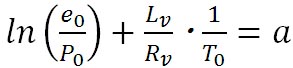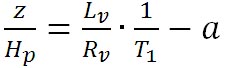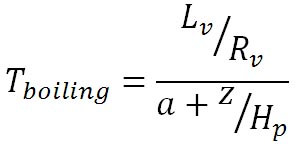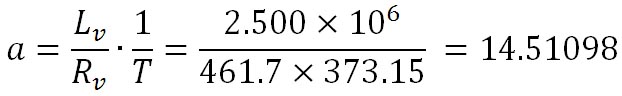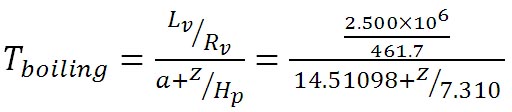高度による沸点変化のグラフを描く
水面や氷面に対する飽和水蒸気圧が温度のみによって定まることを前回までに学び、温度によって飽和水蒸気圧が変化する様子を示す理論式と実験式による計算結果をグラフにしてきた。ところで、この飽和水蒸気圧が周囲の大気圧となる温度が水の沸点に相当する。
この関係を式にすると、大気圧を P 、飽和水蒸気圧を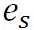 とすると、 とすると、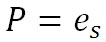 で表される。 で表される。
温度が上昇すると飽和水蒸気圧が急激に上昇したが、その逆に、大気圧が減少すると沸点は下降する。高度が高くなると大気圧が減少することから、高い山に登ると水の沸点は下降する。今回は、水の沸点が高度によって変化する様子をグラフにしてみよう。
最初に、高度と大気圧の関係を式で表そう。高度が上昇すると大気圧は近似的に指数関数的に減少する。その様子は、(片対数グラフを描く)でグラフに示した。すなわち、大気圧 P と高度 z との関係式は、絶対温度で表した大気温を T とすると、以下の式で近似できる。
ここで、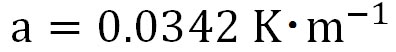 、 、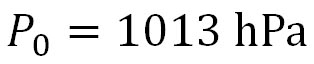 とする。また、実際には気温も高度とともに変化するが、ここでは地上から高度50 kmまでの平均気温を250 Kで一定であるとする。 とする。また、実際には気温も高度とともに変化するが、ここでは地上から高度50 kmまでの平均気温を250 Kで一定であるとする。
上に示した定数を代入して整理すると、以下の式が得られる。
ここで、この式を
の形にしたとき、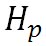 をスケール・ハイト(Scale Height)と呼ぶ。z が をスケール・ハイト(Scale Height)と呼ぶ。z が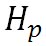 と等しくなると、そこでの気圧は海面気圧の と等しくなると、そこでの気圧は海面気圧の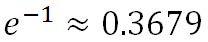 倍に減少し、、さらにその2倍の高度まで上昇すると、そこでの気圧は海面気圧の 倍に減少し、、さらにその2倍の高度まで上昇すると、そこでの気圧は海面気圧の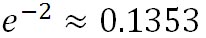 倍に減少する。このように、スケール・ハイトごとに気圧が 1/e ずつ減少する。この高さはe-folding距離と呼ばれるものに相当する。e-folding距離には定訳がないようだが、指数関数の値が 1/e に折りたたまれて減少する距離という意味である。 倍に減少する。このように、スケール・ハイトごとに気圧が 1/e ずつ減少する。この高さはe-folding距離と呼ばれるものに相当する。e-folding距離には定訳がないようだが、指数関数の値が 1/e に折りたたまれて減少する距離という意味である。
大気の平均温度を250 Kとすると、スケール・ハイトは
となる。この高度は、大気の平均温度が高くなると高くなり、大気の平均温度が低くなると低くなる。
飽和水蒸気圧の温度による変化の様子を示す式としては、クラウジウス・クラペイロンの式を用いる。その式は、(飽和水蒸気圧曲線を描く (1))で求めたとおり、以下の式で与えられる。
高度による大気圧の式と飽和水蒸気圧の式とを等置すると、
ここで、次に示すような逆関数の関係を利用する。
すると、元の関係式は下の式のように変形できる。
ここで、右辺の角括弧内の最初の2項は定数であるので、これを定数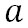 で置き換える。すなわち、 で置き換える。すなわち、
として両辺の対数をとると、次式が得られる。
この式の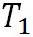 が、高度 z における水の沸点を与えるので、式を整理すると、水の沸点を求める式は以下のようになる。 が、高度 z における水の沸点を与えるので、式を整理すると、水の沸点を求める式は以下のようになる。
ここで、定数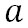 の値は、z=0において水の沸点が摂氏100℃であることから、摂氏100℃を絶対温度に変換した値を代入すると、以下の値が得られる。 の値は、z=0において水の沸点が摂氏100℃であることから、摂氏100℃を絶対温度に変換した値を代入すると、以下の値が得られる。
水の沸点を求める式に、これらの定数を代入すると、エクセルで実際に計算するための計算式が得られ、それは以下の式のとおりである。
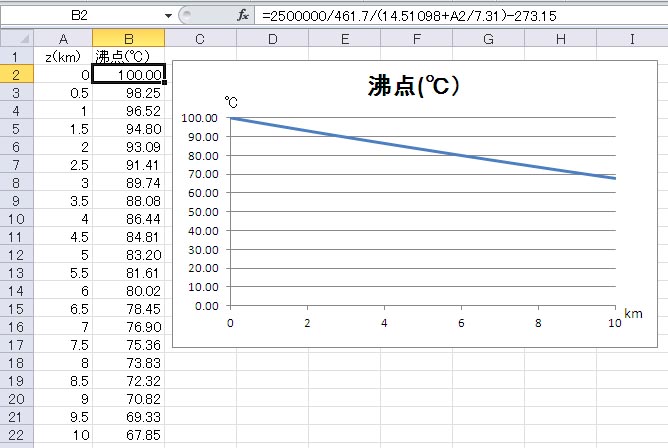
上で得られた式を用いて、高度0 km から 10 km まで、0.5 km 間隔で計算した水の沸点の計算結果を以下に示す。高度 0 km の沸点の計算式が数式バーに見えるが、この式を B列の他のセルにもコピーすれば結果が得られる。グラフとともに計算結果を示した。
最初の 1 km の高度上昇で、水の沸点は約 3.5 ℃減少している。その後、次第に沸点の低下割合は減少し、高度 10 km では約32 ℃の低下となっている。
(2011.3.27)
|