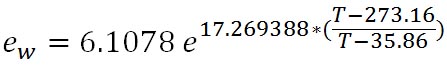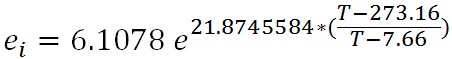|
飽和水蒸気圧曲線を描く (5)
飽和水蒸気圧を計算する実験式の基準とされているゴフ・グラッチの式は、精度は高いとされているが、何としても式が複雑である。これよりずっと簡潔な式でありながら、精度が高い実験式として、マグヌス・テーテンスの式が知られている。その水面に対する飽和蒸気圧
同じく、その氷面に対する飽和蒸気圧
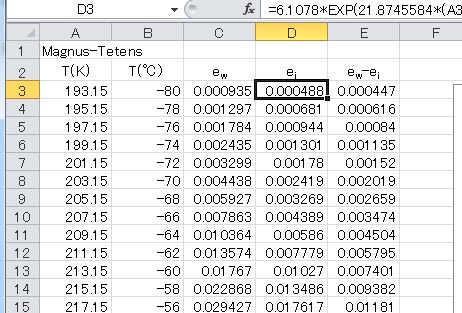
この程度の式であれば、エクセルの数式バーに一気に書き下ろして大丈夫である。これまでと同様に、列 B に摂氏目盛の温度を、オートフィル機能を用いて書き込み、続いて、列Aには、列 B の値に 273.15 を加える式を書き込む。列 C に水面に対する飽和水蒸気圧の計算結果を書き込み、列 D に氷面に対する飽和水蒸気圧の計算結果を書き込むことにする。列 E は、それらの値の差を求めるために用意した。
ここで、C3 セルに書き込んだ式は =6.1078*EXP(17.269388*(A3-273.16)/(A3-35.86))であり、これをそれより下のセルにコピーする。D3 セルに書き込んだ式は =6.1078*EXP(21.8745584*(A3-273.16)/(A3-7.66))であり、これもそれより下のセルにコピーする。E3 セルに書き込んだ式は =C3-D3である。
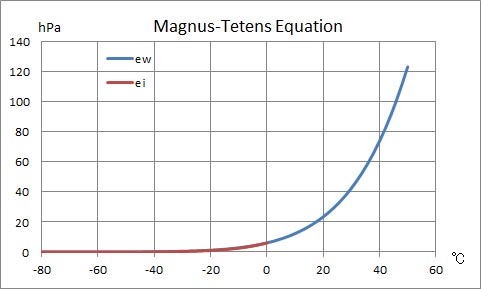
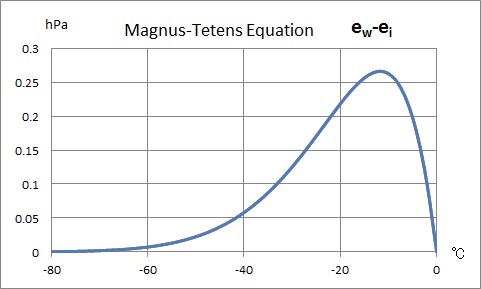
次に、0℃以下の部分について、過冷却水面に対する飽和水蒸気圧から氷面に対する飽和水蒸気圧の値を引いて得られた値のグラフを示す。このグラフの形は、クラウジウス・クラペイロンの式で計算した時の値のグラフに近いものとなっている。
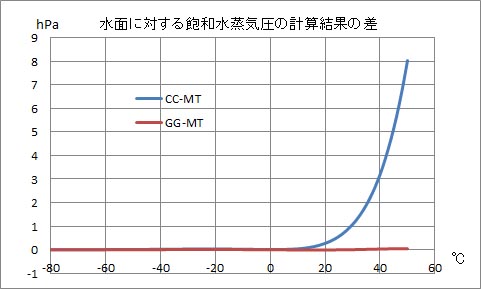
続いて、マグヌス・テーテンスの式の値と、クラウジウス・クラペイロンの式およびゴフ・グラッチの式による計算結果を比較してみよう。これまでに得られた計算結果を、数値だけコピーして、それらの引き算をすれば、比較のグラフは容易に得られる。
上のグラフを見ると、ゴフ・グラッチの式の計算結果とマグヌス・テーテンスの式の値はほぼ一致しているように見える。この結果から、式が簡略なマグヌス・テーテンスの式の実用性が高いことが分かる。一方、温度が高くなると、クラウジウス・クラペイロンの式との値の差が急激に大きくなることが示されている。
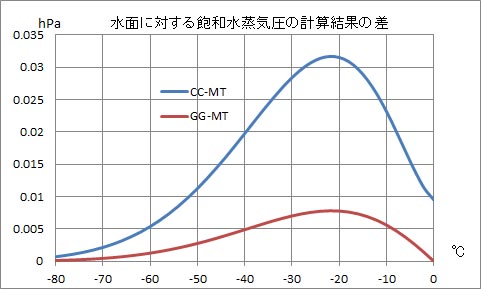
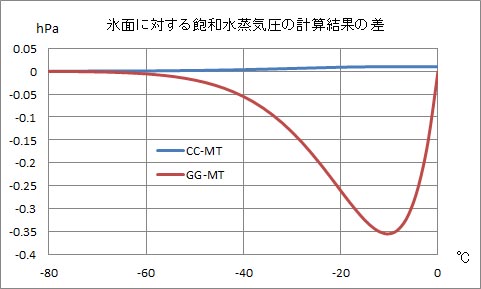
温度0℃以下の部分も、マグヌス・テーテンスの式の値は、クラウジウス・クラペイロンの式の値よりずっとゴフ・グラッチの式との対応が良好なことが分かる。
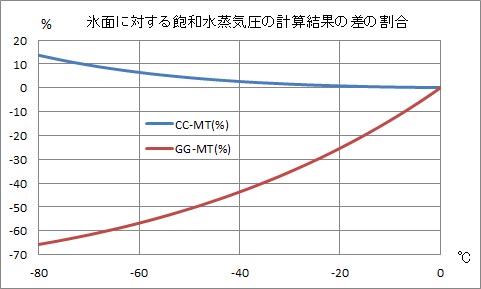
上のグラフは、計算結果の差のグラフであるが、飽和水蒸気圧は温度が下がるときわめて小さな値となり、差の割合は温度が低くなるほど拡大する傾向にある。それを示したのが下のグラフである。このグラフは、前のグラフの値を、その時の温度のマグヌス・テーテンスの式の値で除した値をプロットしたものである。
クラウジウス・クラペイロンの式の値もゴフ・グラッチの式の値も、温度が低下するとマグヌス・テーテンスの式の値との差の割合が増加することが示されているが、クラウジウス・クラペイロンの式の値との対応がずっと良いことには変わりがない。 | ||||||||||