|
飽和水蒸気圧曲線を描く (4)
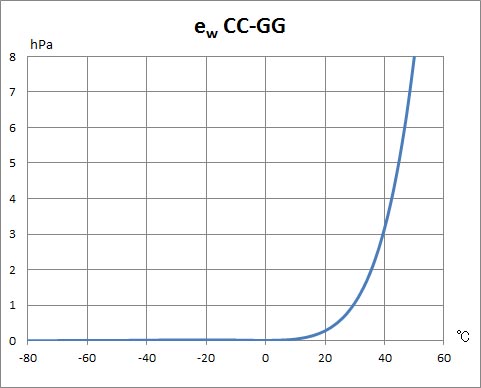
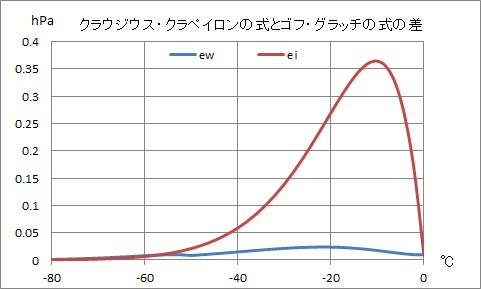
前回は、飽和水蒸気圧と温度との関係を表す実験式の基準式とされているゴフ・グラッチの式を用いて、水面および氷面に対する飽和水蒸気圧を計算し、それらのグラフを描いた。水面に対する飽和水蒸気圧と氷面に対する飽和水蒸気圧との差のグラフも描いた。この、水面に対する飽和水蒸気圧と氷面に対する飽和水蒸気圧との差のグラフは、クラウジウス・クラペイロンの式を用いて作成した同様のグラフと大きく異なる結果となっていた。ここで、両者の計算結果の差を比較してみよう。
このようにして、クラウジウス・クラペイロンの式の計算結果とゴフ・グラッチの式の計算結果をコピーし、水面に対する飽和水蒸気圧の計算結果の差を計算してグラフにしたのが以下の図である。
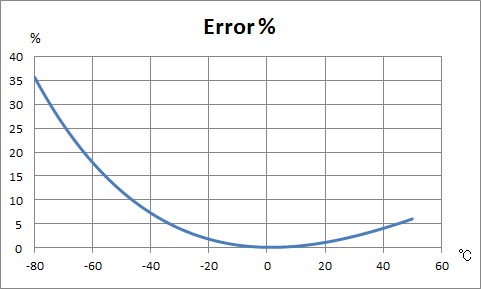
このグラフを見ると、温度の上昇に伴い、両式の計算結果の差が増大していることが分かる。ただし、もともと飽和水蒸気圧の値は、温度の上昇とともに急激に値が上昇する。単に計算結果の差を調べただけでは、計算精度の比較はできない。
前のグラフとはだいぶ様子が異なり、-50 ℃以下の温度の低い部分で、相対誤差は急激に増加していることが分かる。また、0 ℃付近において、相対誤差はきわめて小さく(0.15%程度)なっている。
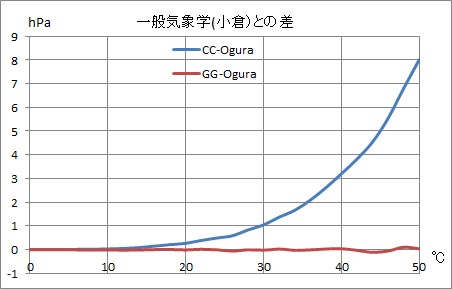
ここで、手元にあるテキストの表の値と比較してみた。小倉義光先生の一般気象学[第2版]のP59には、「表3.3 氷・水面に対する飽和水蒸気圧および飽和水蒸気密度の温度依存性」という表がある。その表の中の飽和水蒸気圧の値をエクセルのセルに打ち込んで比較してみた。下のグラフは、温度0度以上の水面に対する飽和水蒸気圧を比較したものである。
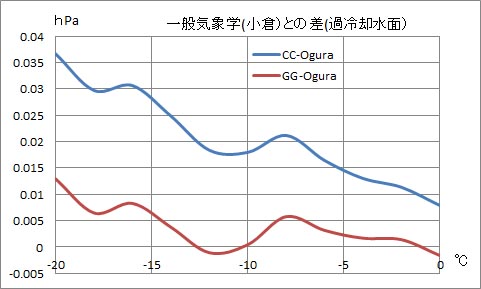
CC-Ogura は、クラウジウス・クラペイロンの式の計算結果から、小倉先生の表の値を引いたものである。GG-Ogura は、ゴフ・グラッチの式の計算結果から、小倉先生の表の値を引いたものである。このグラフから、小倉先生の本の表とゴフ・グラッチの式の計算結果はほぼ一致していることが分かる。
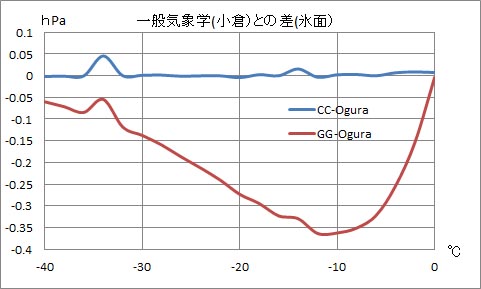
このグラフを見ると、小倉先生のテキストの表の値は、ゴフ・グラッチの式の計算結果に近いことが分かるが、妙な振動を示したグラフとなっている。その振動は、クラウジウス・クラペイロンの式の計算結果との差にも同様な形で表れている。そして、温度が下がるにしたがって、これらの計算結果との差が拡大している。
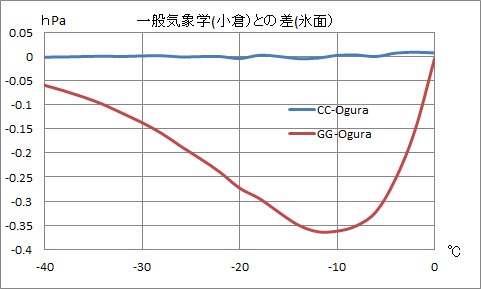
このグラフを見ると、小倉先生のテキストの表の値は、クラウジウス・クラペイロンの式の計算結果とほぼ一致している。-34℃のところに「こぶ」があるが、これは小倉先生のテキストのミスプリントである。手元のテキストの-34℃の値は「0.205」となっているが、これは本来「0.250」となるべきものである。さらに言えば、-14℃のところの値が「1.80」となっているが、これを「1.82」とすれば、この部分にある小さなこぶも取れる。その修正を加えたグラフを下に示す。
以上の比較結果をまとめると、小倉先生のテキストの表3.3の飽和水蒸気圧の表の値は、水面に対する値としてはゴフ・グラッチの式の計算結果に近いが、氷面に対する値はクラウジウス・クラペイロンの式の計算結果とほぼ一致している。 | |||||||||