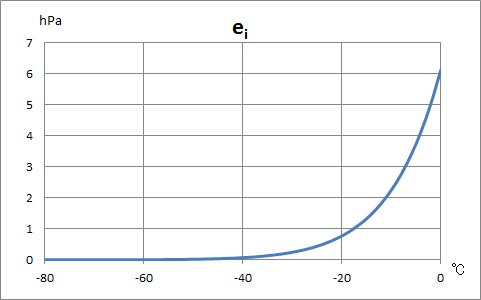
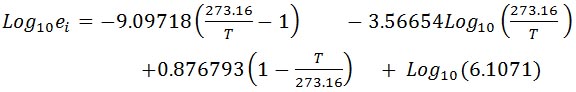飽和水蒸気圧曲線を描く (3)
前回は、飽和水蒸気圧と温度との関係を表す理論式のクラウジウス・クラペイロンの式を用いて、水面および氷面に対する飽和水蒸気圧を計算し、それらのグラフを描いた。水面に対する飽和水蒸気圧と氷面に対する飽和水蒸気圧との差のグラフも描いた。
前回計算したは飽和水蒸気圧は、潜熱が温度によって変化しないと仮定しており、実際の値とは差があるとされる。そこで、実際の飽和水蒸気圧を近似した様々な実験式が提案されてきた。その中でも、1946年にゴフ(Goff)とグラッチ(Gratch)によって発表された実験式は、改訂を経てゴフ・グラッチの式として飽和水蒸気圧を計算する標準的なものとして使用されるようになった。ただ、この式はいささか複雑である。
水面に対する飽和水蒸気圧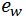 の絶対温度 T に関する関係式を以下のものである。 の絶対温度 T に関する関係式を以下のものである。
この式は、マイナス50℃から102℃まで有効とされている。
氷面に対する飽和水蒸気圧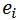 の絶対温度 T に関する関係式は以下のものである。 の絶対温度 T に関する関係式は以下のものである。
いずれも複雑な式で、特に水面に対する飽和水蒸気圧の式は、有効桁数の多い係数が含まれる5項からなる式であり、これをエクセルの関数バーに一気に書き下すと、誤りが含まれる可能性が高くなり勧められない。各項を分けて計算することで、式に誤りが含まれる可能性を減らすことができる。また、各項がどのような値となるのかを見ることができて便利である。
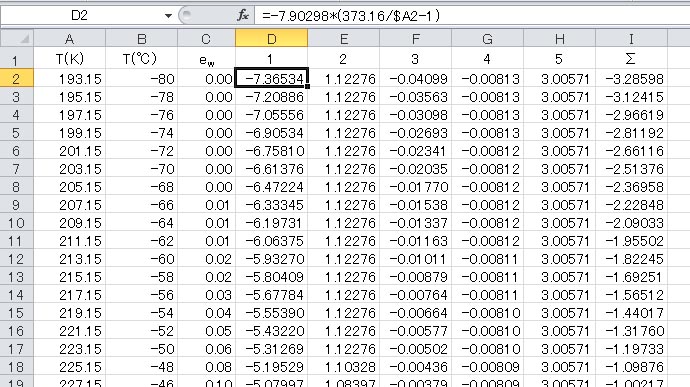
水面に対する飽和水蒸気圧をゴフ・グラッチの式で計算したエクセルの表を以下に示す。
最初に列 B に摂氏目盛の温度を、オートフィル機能を用いて書き込んだ。続いて、列Aには、列 B の値に 273.15 を加える式を書き込んだ。具体的には A2 セルに =B2+273.15 と書き込み、下のセルにコピーした。
列 C には、計算結果を記入する列を用意した。
列 D から列 H は、ゴフ・グラッチの式の各項の値の計算結果を書き込むために用意し、それらの和を書き込む列が列 I である。これら列の2行目に書き込んだ式を下の表に示した。
| セル |
式 |
| C2 |
=10^2 |
| D2 |
=-7.90298*(373.16/$A2-1) |
E2
|
=5.02808*LOG(373.16/A$17) |
F2
|
=-0.00000013816*(10^(11.344*(1-$A2/373.16))-1) |
| G2 |
=0.0081328*(10^(-3.49149*(373.16/$A2-1))-1) |
| H2 |
=LOG(1013.246) |
| I2 |
=SUM(D2:H2) |
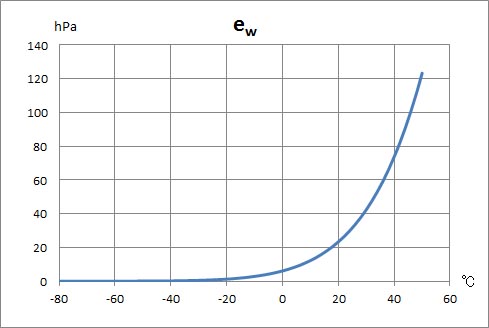
上に示した式を、各列の下のセルにコピーすれば、計算は完了である。計算結果の列 B と列 C を選択して散布図を描いたものに、若干修正を加えたものが以下のグラフである。
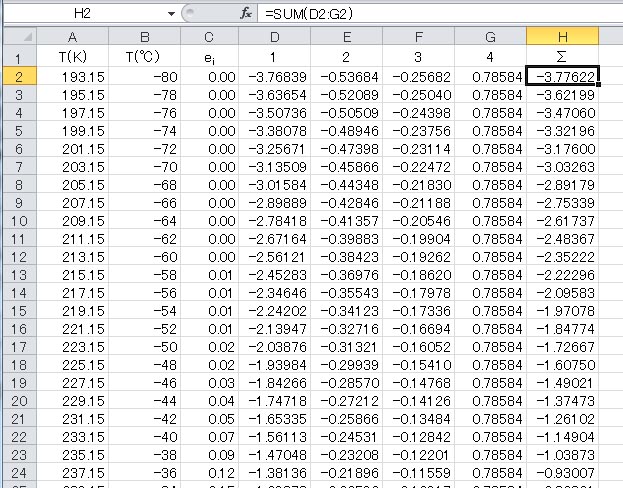
次に、氷面に対する飽和水蒸気圧をゴフ・グラッチの式を用いて計算しよう。その過程は、水面に対する飽和水蒸気圧の計算の時と、ほとんど同様の手続きである。下に、その計算結果を示した。
最初に列 B に摂氏目盛の温度を、オートフィル機能を用いて書き込んだ。続いて、列Aには、列 B の値に 273.15 を加える式を書き込んだ。具体的には A2 セルに =B2+273.15 と書き込み、下のセルにコピーした。
列 C には、計算結果を記入する列を用意した。
列 D から列 G は、ゴフ・グラッチの式の各項の値の計算結果を書き込むために用意し、それらの和を書き込む列が列 H である。これら列の2行目に書き込んだ式を下の表に示した。
| セル |
式 |
| C2 |
=10^2 |
| D2 |
=-9.09718*(273.16/$A2-1) |
E2
|
=-3.56654*LOG(273.16/$A2) |
F2
|
=-0.876793*(1-$A2/273.16) |
| G2 |
=LOG(6.1071) |
| H2 |
=SUM(D2:G2) |
上に示した式を、各列の下のセルにコピーすれば、計算は完了である。計算結果の列 B と列 C を選択して散布図を描いたものに、若干修正を加えたものが以下のグラフである。
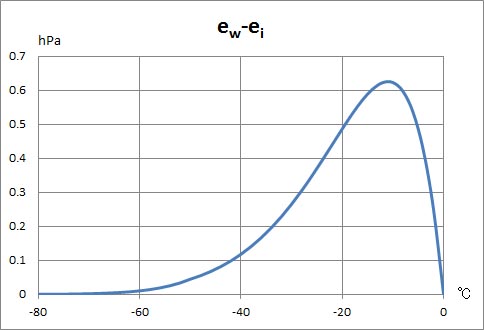
続いて、過冷却水面に対する飽和水蒸気圧と氷面に対する飽和水蒸気圧の差の温度による変化を示すグラフを以下に示す。
このグラフは、前回作成したクラウジウス・クラペイロンの式による計算結果のグラフとはずいぶん異なる。前回得られたグラフでは、最大値が0.3 hPaを下回っていたのに、今回のグラフでは最大値は0.6 hPaを上回っており、2倍以上の差が生じている。このような大きな差が生じた理由は、過冷却水面に対する飽和水蒸気圧の値の影響は少なく、氷面に対する飽和水蒸気圧の計算結果が、クラウジウス・クラペイロンの式とゴフ・グラッチの式との間で、大分異なるからである。
| 
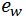 の絶対温度 T に関する関係式を以下のものである。
の絶対温度 T に関する関係式を以下のものである。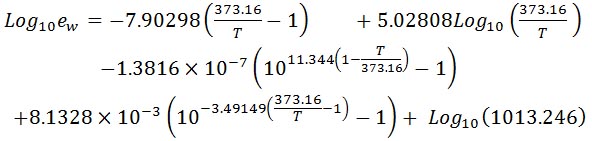
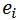 の絶対温度 T に関する関係式は以下のものである。
の絶対温度 T に関する関係式は以下のものである。