これまで、海面気温が地球の緯度によってどのように変化するか、モデル式と気象庁のデータに基づく観測値をエクセルのグラフで描いてみた。この例では、地球の緯度を横軸に、海面気温を縦軸にしてグラフを描いた。緯度が変化すると、気温がどのように変化するかを理解するのがこのグラフの目的である。したがって、地球の緯度が説明変数（独立変数）となり、海面気温が目的変数（従属変数）となっている。

　描いたグラフでは、説明変数を横軸（Ｘ軸）に、目的変数を縦軸（Ｙ軸）にした。一方、地球上の気温は高度によっても大きく変化する。この、地球上の高度による気温の変化の様子を描くグラフでは、高度が説明変数で、気温が目的変数となろう。ただ、高度を横軸にし、気温を縦軸にして描いたグラフには違和感を感じる。高さ方向は、縦軸という一般的な感覚があるからだ。

　地球の高さ方向の気温や気圧の値のような、大気の状態を示す各種のパラメーター（変数）は、大気構造を示す変数である。大気構造は、天気や太陽活動によって変化するが、その標準的な値を知ることは航空機の運航や人工衛星の軌道計算などでは欠かせない情報で、古くから表にまとめられてきた。

　その後も、大気構造の精密化は進められているが、「1976年の米国標準大気モデル」は、今でも一つの標準となっている。それは、この標準が長く使い続けられることを想定して作られたからである。この標準大気モデルは、定常状態にある理想状態の乾燥大気の、高度による状態変化を示している。このモデルが示す各変数の値が、大気の平均的な状態と考えることができる。

　このモデルが用いている高度は、通常の高度（幾何学高度）ではなくジオポテンシャル高度というものである。地球上の重力加速度は高度とともに減少するが、それを補正して、どこでもという標準の重力加速度の値を用いることができるようにしたのがジオポテンシャル高度である。

　ジオポテンシャル高度H は、地球の半径を とすると、 となる。ここで、z は幾何学高度と呼ばれる普通の高度である。ジオポテンシャル高度と幾何学高度の差は、高度とともに拡大するが、地球の半径に比べて高度の値が小さければ、その差は小さい。ちなみに、高度10 kmでは、これらの間には0.157 % の差しかなく、すなわち15.7 m しか違わない。

　地球の上空に行くにしたがい、同一場所のジオポテンシャル高度の値は幾何学高度よりも小さくなる。ということは、ジオポテンシャル高度が示している場所は、数値が同一の幾何学高度が示している場所より高いということである。上空に行くにしたがい重力加速度は減少するが、それがずっと標準の重力加速度として考えて積み上げた高度であるから、重力加速度が減少する分だけ、さらに高い位置まで積み上げる必要があるからだ。

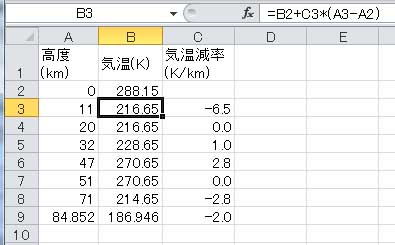
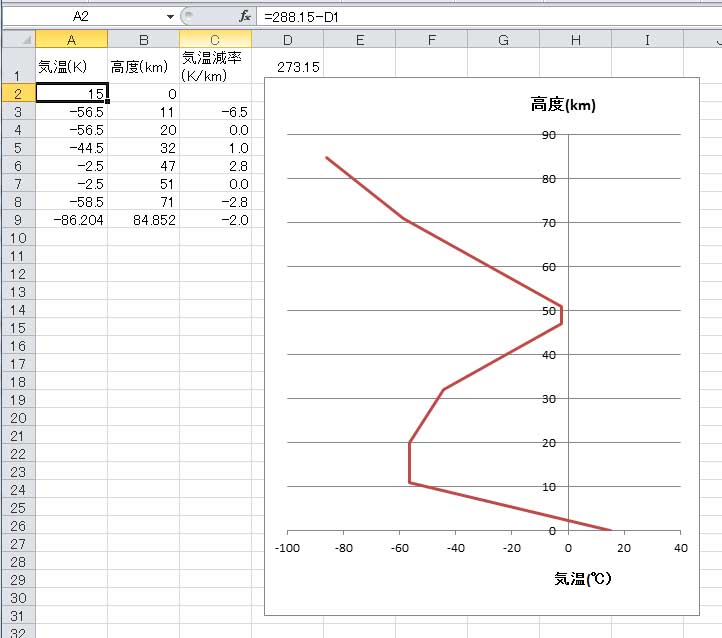
　上の表は、1976年の米国標準大気モデルが用いている気温の計算条件である。なお、地上の気温は288.15 K=15.0 ℃ としている。上の表で、層１が対流圏、層２～４が成層圏、層５～７が中間圏に相当する。ジオポテンシャル高度84.852km は、幾何学高度86 km に相当する。気温減率とは、高度1 km　当たりの気温変化量を示し、マイナスの値は、上空に行くにしたがって気温が減少することを示し、プラスの値は上空に行くほど気温が高くなることを示す。

　この標準大気モデルの気温のグラフを描いてみよう。

　エクセルのシートに書き込むデータは簡単なものである。
　A1セルに「高度(km)」と書き込み、その下のセルから順に、大気層の限界値である0、 11、20、32、47、51、72及び84.852と書き込む。
　B1セルに「気温(K)」と書き込み、B2セルに288.15と書き込む。 　C1セルには気温減率(K/km)と書き込み、C2セルは空白にして、以下、-6.5、0.0、1.0、2.8、0.0、-2.8及び-2.0と書き込む。
　計算式は、B3セルに=B2+C3*(A3-A2)と書き込み、B9セルまで下にコピーする。

　上の図は、ここまでやった状態を示す。

　続いて、A1セルからB9セルまでを選択し、「挿入」「散布図」「散布図（直線）」を選択すると、下のようなグラフが描かれる。

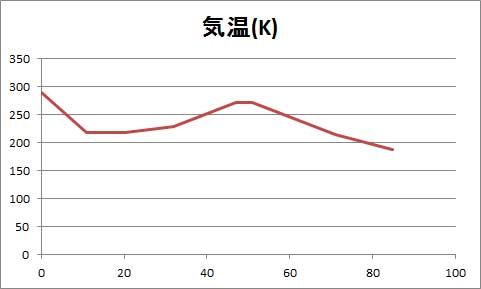
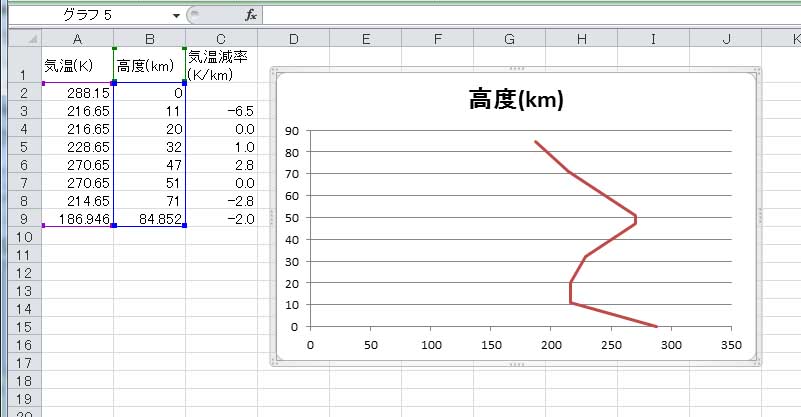
　確かに、気温の変化を示すグラフにはなっているが、横軸に高度が来ており、よく見かける気温の高度変化を示すグラフとは異なってしまった。エクセルの散布図は、選択範囲の1列目のデーターがX軸に、2列目のデーターがY軸に来るので、このようなグラフとなる。 　そこで、よく見かけるグラフと同じものを作るには、A列とB列を交換すればよい。

　そのようにして出来上がったのが上に示すグラフである。グラフの格好は教科書でよく見るものに比べると上下方向につぶれているが、ほぼ同じものだ。ただ、列Bの表題がグラフの表題となってしまった。

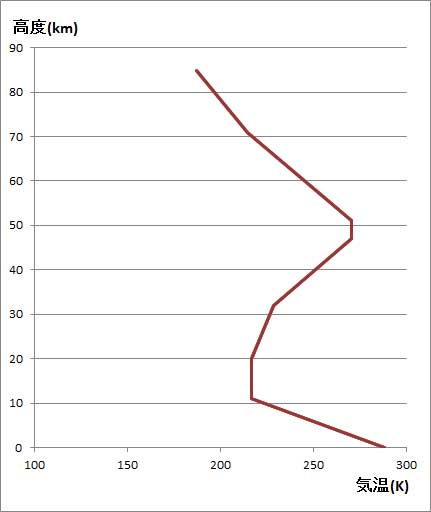
　そこで、軸の書式を若干調整して完成したのが、上のグラフである。気象学の教科書で見るグラフと似たものとなった。

　さらに、温度の単位を、日常生活で親しみのある摂氏に変換したものが上の図だ。D1セルに、摂氏零度の絶対温度である273.15を書き込み、A2セルを=288.15-D1と書き換えただけだ。高度の軸目盛は、軸の右側に付けたいところだが、エクセルでは目盛を軸の右側の付けるオプションはないようだ。

　これで、目的変数が縦軸方向のグラフが完成した。

　標準大気モデルは、緯度45 °の中緯度地方を対象として作られている。以前グラフを示した子午線気温を計算したモデル式で、海面気温が15 ℃の緯度を探してみると42.5 °となっている。

　1976年大気モデルと、その前身である1962年大気モデルとで異なるのは高度51 kmを超える部分である。このような高度の大気温は、ソヴィエトのM-100ロケットによる白金抵抗センサー観測値に負うところが大きい。ソヴィエトの観測データは、空気抵抗によるセンサーの温度上昇や太陽の放射熱などの影響を補正した良質のデータだった。このような補正を行った観測値と、これまでのデータの差は、高度40kmでは1～2 Kであったが、高度55 kmを超えた部分ではかなりの大きさとなった。1976年大気モデルでは、高度60 km以上では、ソヴィエトの観測値に合わせて、1962年のデータより下げられた。

　ここで示されている気温は、年間の平均値である。1年を通じての気温変化は、1年を周期としたサインカーブと半年を周期としたサインカーブを重ねたものとして近似された。そして、これらの平均値が求められた。高度60 km以下では、夏場に最高気温が観測され、高度65 km以上では、冬場に最高気温が観測された。これらの中間は、年間を通じて気温の変化が少ない高度となっていた。