自由対流高度

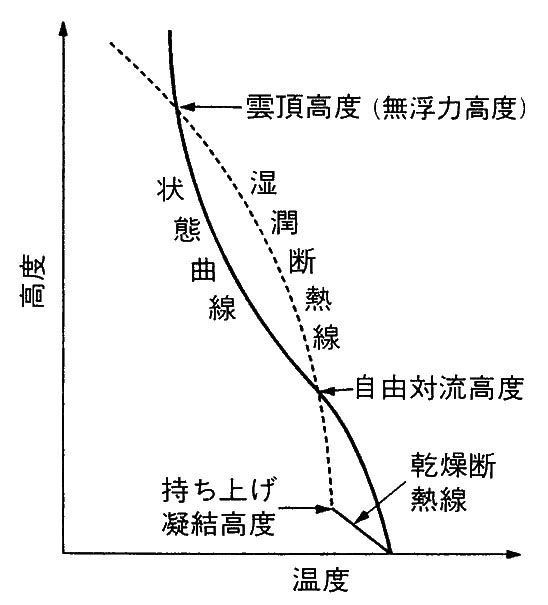
　積雲や積乱雲のような対流性の雲が発達する過程を説明する図は、細かい点や用語の相違はあるにしても、国内の各種の教科書に同等の図が描かれている。下に示した図は、その中から小倉義光先生の「一般気象学（第２版）」のものである。

　ここで注目するのは、持ち上げ凝結高度と自由対流高度の順番である。国内の教科書では上の図のように、持ち上げ凝結高度の方が低く、自由対流高度の方が高い図しか見たことがない。この場合、対流性の雲の雲底高度が最も低く、その位置では自発的な上昇気流は生じておらず、何らかの強制流によって対流活動が起きていることになる。そして、雲底高度と雲頂高度の間の位置で、自発的な上昇気流が発生し、対流活動が活発化することになる。

　上昇気流が生じているところで、ある程度以上空気が冷えると雲が生じ、凝結の潜熱の放出によって次第に上昇気流が強くなって対流性の雲が発達する、と考えた方が自然ではないかと思うのは私だけであろうか？ところで、国外の教科書では事情は異なるようである。アーレンの教科書を見ると、自由対流高度の方が持ち上げ凝結高度より低い解説図が載せてある。今回は、アーレンの模式図をエクセルのグラフにしてみよう。

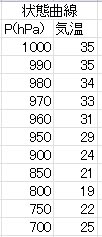
　アーレンの教科書には、細かい数値が省略されている部分があるが、図を参照して状態曲線として、以下の表に示した値を入力した。地上の気温は35 ℃で、露点温度は27 ℃である。800 hPaの高度まで気温は低下し、その後、下降気流によって気温の上昇がみられる。

　上に示した状態曲線のデーターを、以前作成したエマグラムに追加し、さらに交点に対応する等飽和混合比線と湿潤断熱線を追加して描いたグラフを以下に示す。

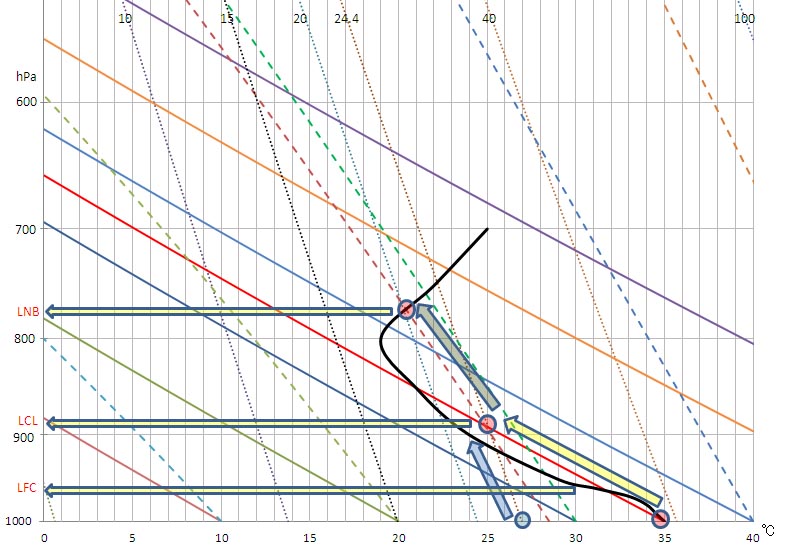　1000 hPaで35 ℃を通過する乾燥断熱線と状態曲線は32 ℃のところで交わり、その高度は966 hPaである。すなわち、自由対流高度(Leve of Free Convection - LFC)は966 hPaであり、標準大気では約300 mの高度となる。この高度をエマグラムから正確に読み取るのは難しいが、乾燥断熱線を計算している表の縦軸の高度の欄の値を、気温が32 ℃となるように試行錯誤的に入力することで、容易に求められる。

　この空気塊は、この高度から上空では浮力を得て自発的に上昇し、乾燥断熱線に沿って気温は低下する。1000 hPaで27 ℃を通過する等飽和混合比線の混合比は24.4 g/kgである。その等飽和混合比線が上のエマグラムには記入してある。1000 hPaで35 ℃を通過する乾燥断熱線と、混合比が24.4 g/kgの等飽和混合比線とは、25 ℃のところで交わる。この点が持ち上げ凝結高度(Lifting Condensation Level - LCL)となる。この高度も、エマグラムから正確に読み取ることは難しいが、やはり、等飽和混合比線の計算の表で、混合比24.4 g/kgの線が25 ℃となるように、試行錯誤的に値を代入すると、890 hPaであることが分かる。

　持ち上げ凝結高度は雲底高度に相当するが、この点では空気塊は十分な浮力を得ており、自発的に上昇を続ける。空気塊は水蒸気で飽和しているため、ここから上は、湿潤断熱線に沿って気温が低下していく。持ち上げ凝結高度の点を通過する湿潤断熱線は、1000 hPaで28.5 ℃を通過するが、その湿潤断熱線も、上のエマグラムには記入されている。露点温度も、この湿潤断熱線に沿って低下していく。800 hPaから上方では、下降気流によって周囲の気温が上昇している。その様子は状態曲線がそこから右に大きくカーブしていることで示されている。空気塊が20.5 ℃まで冷却されたところで、湿潤断熱線と状態曲線とは交差し、空気塊の気温よりも周囲の気温の方が高くなり、空気塊は浮力を失う。この点が無浮力高度（Level of Neutral Buoyancy -LNB)で、雲頂高度に相当する。

　この高度も、エマグラムからは細かく読み取るのは難しい。また、湿潤断熱線は逐次計算をしているため、縦軸の値を指定して、その場所の温度を計算することは容易ではない。そのため、目分量で値を求めることになるが、その高度は約780～790 hPaと読み取ることができる。一方、この湿潤断熱線と状態曲線との交点を通過する等飽和混合比線は、ほぼ20 g/kgの等飽和混合比線である。この等飽和混合比線の計算表の高度に、試行錯誤的に値を代入して、温度が20.5 ℃になる高度を求めると785 hPaである。

　以上、エマグラムを用いて、自由対流高度より持ち上げ凝結高度の方が高い場合の対流性雲の生成について調べてきた。得られたエクセルのグラフから、不要な線を消去して、模式図に変換した図を以下に示す

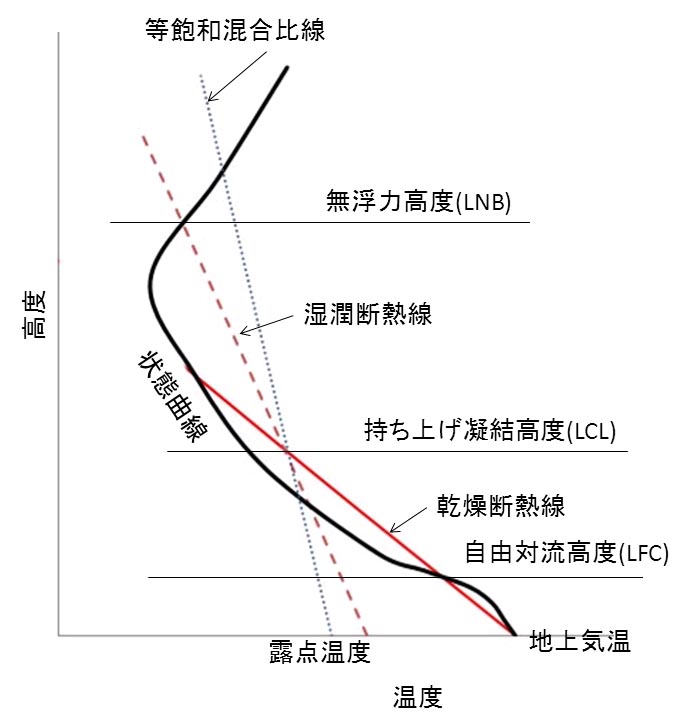　見慣れた模式図と比べて、間の抜けた感じの図となった。対流有効位置エネルギー（CAPE)がどこかだかよくわからない図となっているからである。

(2011.4.27)