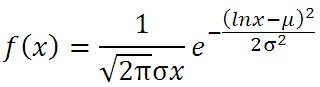雲の大きさと対数正規分布

　空に浮かぶ雲には、さまざまな形と大きさのものがある。地上から見ると、高い所にある雲は小さく見え、低い雲は大きく見えるが、実際の大きさはどのくらいなのだろうか？雲の種類によって大きさもさまざまであることから、一概にはいえないだろうが、積雲の例がシュトゥールの教科書に紹介されている。積雲は、その直径と高さがほぼ等しい形状をしていて、好天時の空に浮かんでいる積雲の直径は約1 km、発達した積乱雲では、直径が10 kmにも及ぶだろうということである。ただ、種類が同じ雲であっても大きさには変動があり、対数正規分布をしているという。

　対数正規分布とは、その分布にしたがう確率変数の対数を取ると正規分布となる分布のことで、次のような性質がある。

(1)値域は正の値となる。　　－＞　雲の大きさは常に正で条件に合う。
(2)モード(分布の山の頂上の位置）が平均値より小さい。
(3)飛び離れて大きな値を取ることがある分布に適合する。

　対数正規分布の確率密度関数は次式で与えられる。

　ここで、μとσは、この分布の平均値と標準偏差を表さず、この分布の対数を取って得られる正規分布の平均値と標準偏差となる。対数正規分布の確率密度関数の形状は、μとσの値の選び方で大きく変化する。したがって、雲の大きさの分布が対数正規分布にしたがうといっても、観測結果によって適切なμとσを選択することが重要となる。

　エクセルでは、対数正規分布の累積分布関数と確率密度関数を計算するLOGNORM.DISTという 関数が用意されている。この関数には４つの引数があり、

　　　　　　　　LOGNORM.DIST(x、平均、標準偏差、関数形式)

という形式で指定する。ここで、xは、関数を計算する横軸の値である。平均はμのことであり、先に説明したとおりln(x)の平均値である。標準偏差はσのことであり、ln(x)の標準偏差である。関数形式は、TRUEを指定すると累積分布関数の値が計算され、FALSEを指定すると確率密度関数の値が計算される。

　ここでμとσの値を５種類の組み合わせで指定して、対数正規分布の確率密度関数を計算した結果を以下に示す。

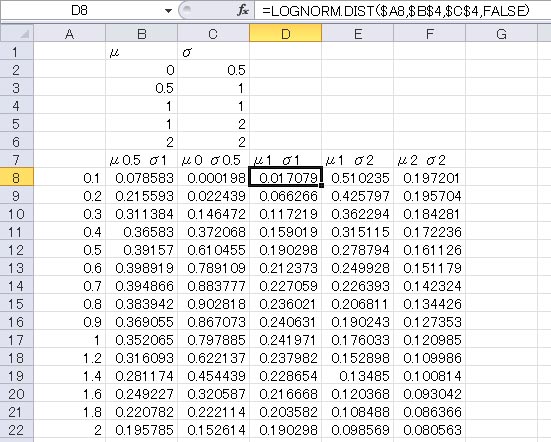
　どのような形の分布をしているかは、グラフにすると分かりやすい。このグラフから、μとσの値によって、確率密度関数の形状がさまざまに変化していることが分かる。

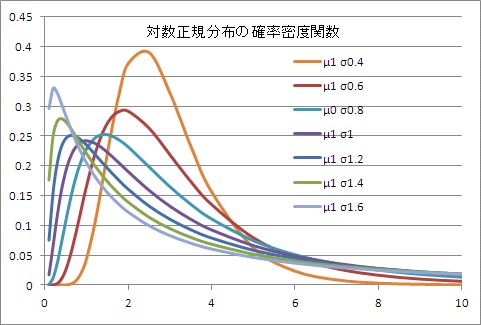
　次に、μを１に固定し、σを0.4から1.6まで、0.2刻みで変化させて確率密度関数の変化を調べたのが、以下のグラフである。このグラフを見ると、σが大きくなるにつれて、ピークの位置が左にずれて、グラフの左右の非対称性が大きくなっている。その逆にσが小さくなるにつれて、ピークの位置が右にずれ、グラフの左右の非対称性が小さくなることが分かる。ピークの高さは、σが１の時に一番低くなっている。

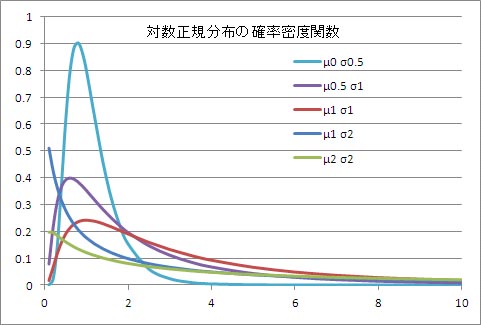
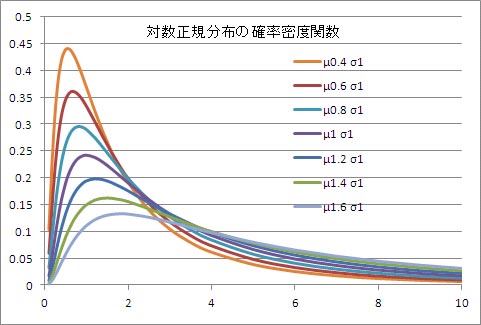
　次に、σを１に固定して、μを0.4から1.6まで、0.2刻みで変化させて確率密度関数の変化を調べたのが、以下のグラフである。μが大きくなるにつれてピークは低くなり、ピークの位置が右にずれ、右に行くにしたがう減少程度が小さくなっている。その逆にμが小さくなるにつれて、ピークが高くなり、ピークの位置が左にずれ、右に行くにしたがう減少程度が大きくなっている。

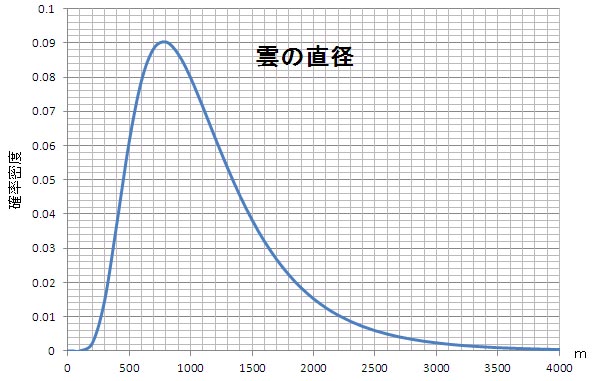
　雲の大きさの分布を対数正規分布で近似するには、観測に基づいてμとσの値を定める必要がある。ただ、この値は、時と場所によって大幅に変化するとされている。その一例が、シュトゥールの教科書の練習問題にみられる。そこで計算しているのは、μの値として1000 m、σの値として0.5が選ばれている。そして、雲の直径の確率密度を100 m間隔で、ヒストグラム表示している。それを連続した確率密度にして示したグラフを以下に示す。

　この例では、雲の直径のモード（最頻値）は約800 mとなっている。

　実際の雲の直径に値を合わせると、横軸の値が大きくなっていしまい、通常の対数正規分布の確率密度を計算するのに適さなくなる。そこで、確率密度の形状を試行錯誤的に合わせたところ、μ=1.9、σ=0.5の分布と形状が一致した。その確率密度関数のグラフを以下に示す。

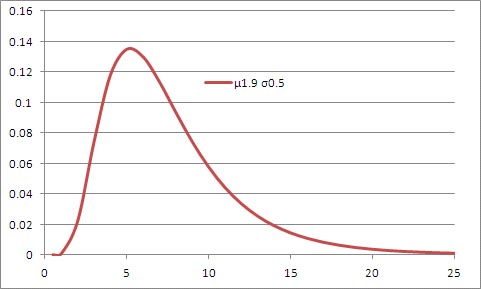
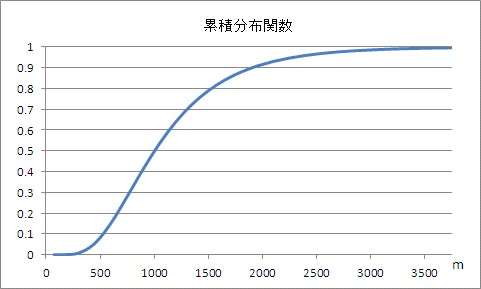
　このグラフのμ=1.9、σ=0.5のパラメーターを用い、横軸をメートルに変換し、LOGNORM.DIST関数の最後の引数をTRUEにして描いた累積分布関数を以下に示す。

　このパラメーター設定では、雲の直径が3000 mまでの累積分布は98.6 %となっている。このことから、このパラメーター設定では、雲の直径が3 kmを超える積雲が1.4 %の割合で発生することを示している。

(2011.5.1)