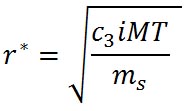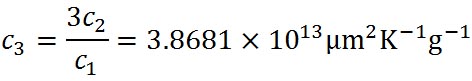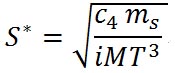|
微小水滴形成への溶質の影響 (2)
このグラフは、溶質の質量を
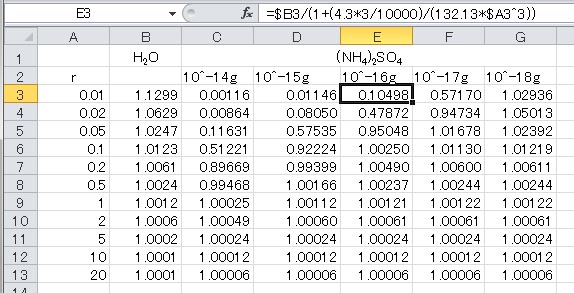
この表から、半径が0.1μmの水滴に質量
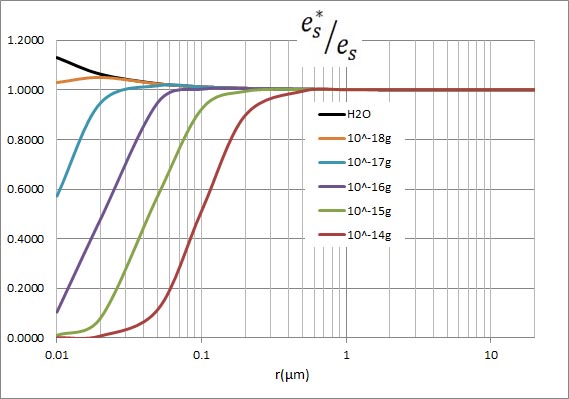
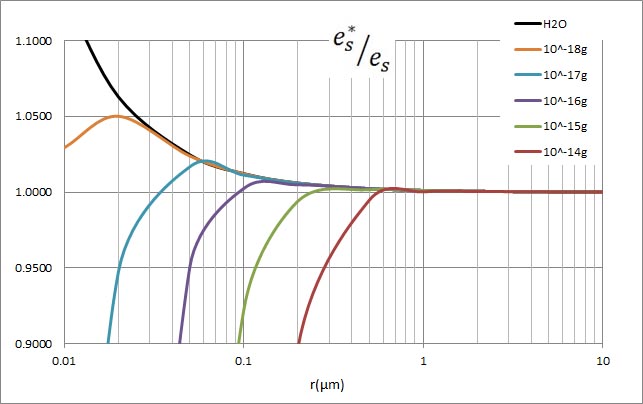
上の計算結果をグラフにしたものを以下に示す。溶け込んでいる溶質の量が減少すると、
水滴の半径が小さい場合の飽和水蒸気圧の減少が開始する半径が小さくなることが分かる。
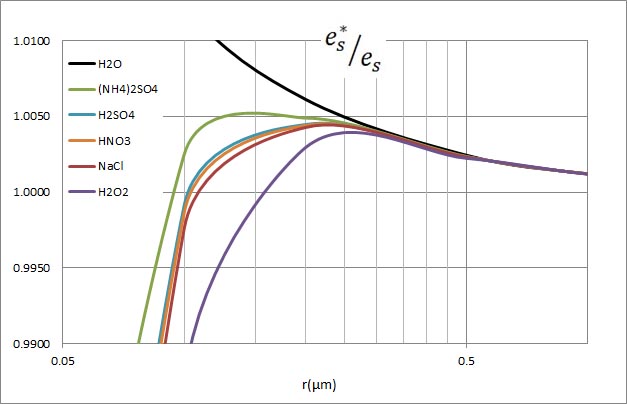
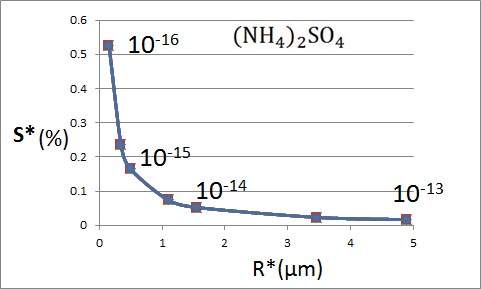
飽和蒸気圧が減少し始める部分を拡大したものが以下のグラフである。このようなグラフが掲載されている書物を見ることがある。溶け込んでいる溶質が少なくなると、過飽和度の極大値が高くなっている。そして、実際の大気で水蒸気の過飽和度が0.1 %程度であるとするならば、10のマイナス15乗グラム程度の溶質が含まれているはずであると説明されている。
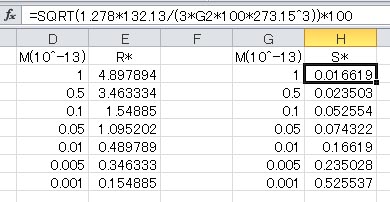
飽和水蒸気圧の極大値は、ケーラーの式を微分して0となる場所である。式の展開はシュトゥールの教科書にあり、ここでは省略する。溶質の質量に対する極大となる水滴の半径は以下の式で与えられる。
ここで、
であり、その時の過飽和度(相対湿度)は次の式で与えられる。
ここで、 である。この式を用いて、溶質の質量を10のマイナス13乗からマイナス16乗まで、摂氏0度で硫酸アンモニウムについて計算した表を以下に示す。
上に示した計算結果をもとに描いた散布図が以下のグラフである。この計算結果は、先に硫酸アンモニウムの計算結果を用いて拡大して示したグラフの値と一致していることが分かる。
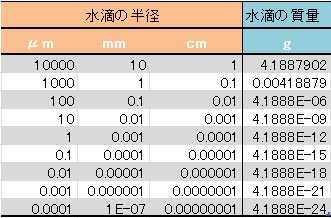
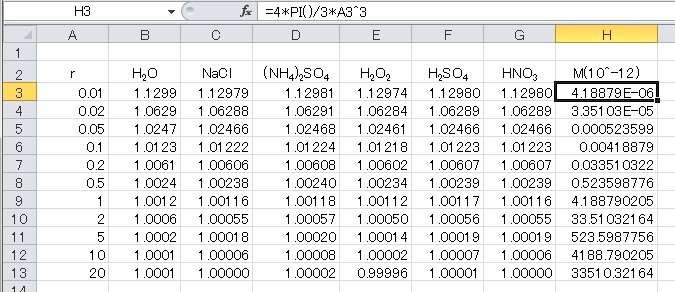
ところで、最初に説明したとおり、水滴の半径が小さくなると、その容積が小さくなるのだから、それに溶け込むことのできる溶質の量も少なくなる。以下の表は、水滴に溶け込んでいる溶質の質量を、水滴の質量と等しくして計算した場合の飽和水蒸気圧である。列Bに、純水の飽和水蒸気圧を示してある。この計算結果を見ると、驚くことに、水滴の質量と見合った量の溶質が溶け込んでいる場合でも、飽和水蒸気圧は純水の場合の飽和水蒸気圧からほとんど低下していない。
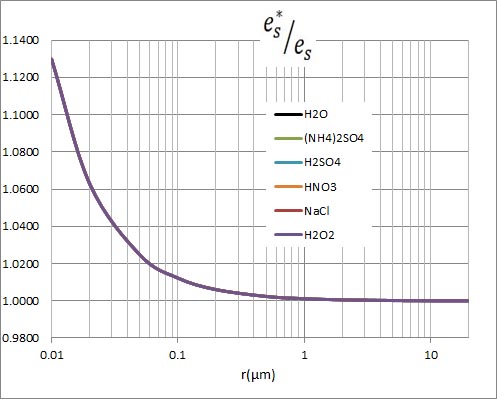
計算結果を見れば、これらのグラフがすべて重なってしまうことは明らかだが、とりあえずグラフを示す。値の相違はグラフの線の幅以下である。すなわち、水滴中に水滴の質量と同量の溶質が溶け込んでいても(ここでは、溶質の比重を水の比重と等しいという近似をした)、飽和水蒸気圧の低下は誤差範囲である。
実際はどうなっているのだろうか?
| ||||||||||||||