煙霧と霞の成長
雲粒の凝結核(Cloud Condensation Nuclei)は、その頭文字をとってCCIと略称される。この雲粒の凝結核は、空気中に浮遊している微粒子であり、エーロゾル(aerosol)とも呼ばれる。エーロゾルは、大気中に浮遊する微細な固体と液体のすべてを指し、雲粒の凝結核となる。乾燥した凝結核に水分子が凝結して、そのサイズが飽和水蒸気圧平衡状態にまで成長する過程をエーロゾル膨潤(Aerosol Swelling)という。汚染した大気の相対湿度が70~80 %程度以上になると、エーロゾル膨潤によって視程障害が発生するとされる。
その状況をシュトゥールの教科書が例題で示している。その例題では、溶質となる硫酸アンモニウムが 0 ℃で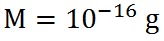 だけ存在する場合、相対湿度が70 %から80 %へと増加した際、煙霧(Haze)の粒の半径がどのように変化するかを求めるものである。 だけ存在する場合、相対湿度が70 %から80 %へと増加した際、煙霧(Haze)の粒の半径がどのように変化するかを求めるものである。
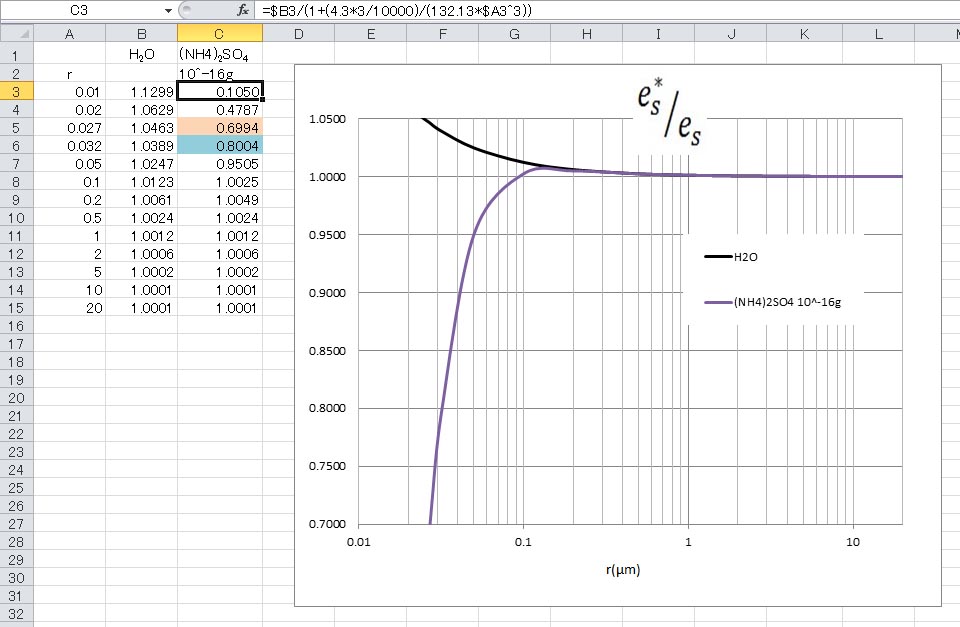
シュトゥールの教科書では、その値はグラフから読み取っているが、エクセルで計算した結果とグラフを以下に示す。
グラフからは、相対湿度の値から煙霧の粒の半径を読み取るのだが、計算するときは、半径の値から相対湿度が計算される。列Cに相対湿度の計算結果が示されており、煙霧の半径が0.027 μmで相対湿度は約70 %、煙霧の半径が0.032 μmで、相対湿度は約80 %となっている。
この結果から、相対湿度が増加すると、煙霧の粒の半径が増大し、その結果として視程障害が増大すると解説されている。この粒の半径を2倍した直径の値は、光の波長と同程度であることから、太陽光はこの粒によってミー散乱(Mie Scattering)する。
シュトゥールの例題では、このエーロゾルに、どれだけの分子が含まれているのかも求めている。そして、相対湿度70 %のときには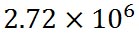 個、相対湿度80 %のときには 個、相対湿度80 %のときには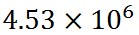 個との答えを示している。 個との答えを示している。
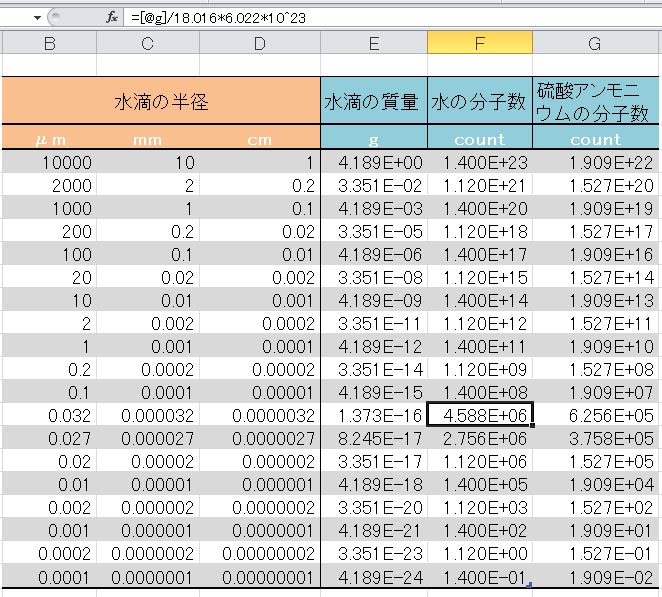
アボガドロ数を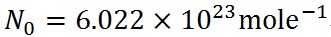 、水の分子量を18.016、硫酸アンモニウムの分子量を132.13として、それぞれの分子数をエクセルで計算した結果を、以下に示す。 、水の分子量を18.016、硫酸アンモニウムの分子量を132.13として、それぞれの分子数をエクセルで計算した結果を、以下に示す。
この計算結果のうち、水滴の半径が0.027μmと0.032 μmの水の分子数の計算結果は、シュトゥールの教科書の値とほぼ一致している。この半径0.027 μmの水滴が蒸発せずにいるためには、これに硫酸アンモニウムが0 ℃で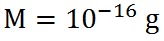 だけ溶け込む必要がある。 だけ溶け込む必要がある。
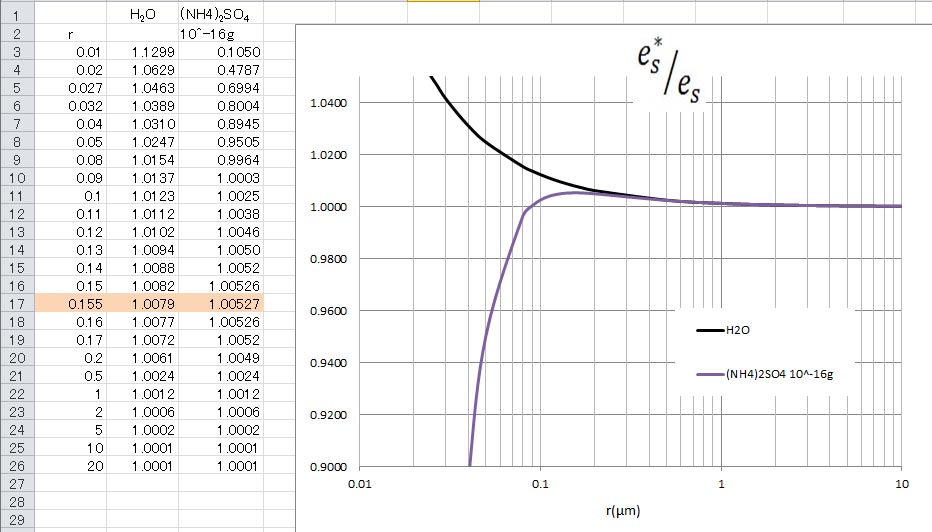
ケーラー曲線は、左側から右へ、相対湿度の増加に伴ってエーロゾルの粒径が増加していくことを示している。そして、その曲線はやがて相対湿度の極大値を示し、その後は右に行くにしたがってグラフは緩やかに低下していく。ここに至ると、エーロゾルの粒径は、大気中に水蒸気が存在する限り、どんどん増加することを意味している。このような状態となった凝結核は活性化凝結核(Activated Cloud Condensation Nuclei)と呼ばれ、これより大きくなったエーロゾルは雲粒(Cloud Droplets)と呼ばれる。
大気中の汚染物質の種類や濃度は多種多様なため、活性化凝結核になる条件は様々だという。ここでは、0 ℃で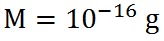 の硫酸アンモニウム溶質の場合を調べてみた。 の硫酸アンモニウム溶質の場合を調べてみた。
上の計算結果で示されているように、粒半径0.155 μmのときに相対湿度が極大となり、これより粒半径が大きくなると凝結核は活性化する。海上、陸上、郊外、都心などで条件は様々だというが、活性化凝結核の数は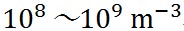 程度あるとされる。一方、エーロゾルの総数は、海洋上で 程度あるとされる。一方、エーロゾルの総数は、海洋上で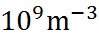 、陸上で 、陸上で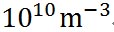 、市街地で 、市街地で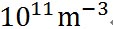 程度とされている。したがって、エーロゾル全体の数に比べれば、活性化凝結核の数はきわめて少ない。 程度とされている。したがって、エーロゾル全体の数に比べれば、活性化凝結核の数はきわめて少ない。
雲粒の間隔は活性化凝結核の密度の三乗根をとることで求められ、それは1 mmのオーダーの距離となる。活性化凝結核の数が1立方メートル当たり10の8乗個の場合で、雲粒の間隔は約2.2 mm、同じく1立方メートル当たり10の9乗個の場合には、雲粒の間隔は1.0 mmとなる。
(2011.5.14)
|