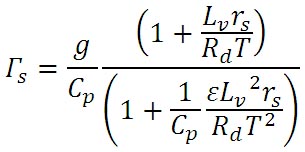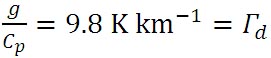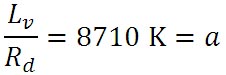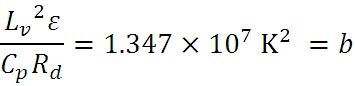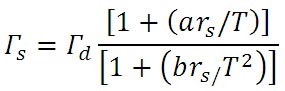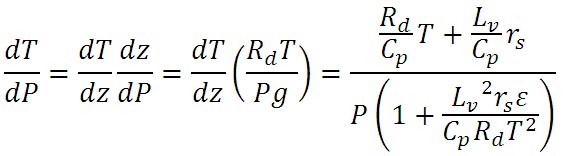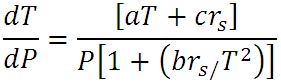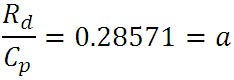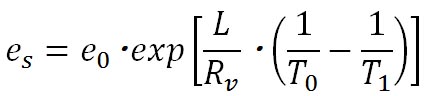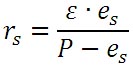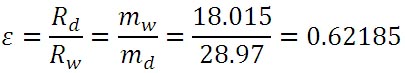得られた式は少し複雑である。この式中の定圧比熱は、湿度（混合比）によって変化する。ただ、それを常に乾燥空気の値を取るとする近似をして定数扱いすると、式を簡略表示できる。まず右辺の最初の項は、乾燥断熱減率に等しく、以下のような定数となる。

　次に、乾燥空気の気体定数を、水から水蒸気、水蒸気から水へと相変化する際に吸収あるいは放出される潜熱をとすると、湿潤断熱減率の式中の分子にある定数を、以下のようにまとめることができる。

　右辺の分子中にある定数を計算すると、以下の値が得られ、これもまとめることができる。

　これらの定数を係数で置き換えると、湿潤断熱減率を求める式は以下のように簡略表示できる。

　それでも、飽和混合比が気温とともに変化することから、この式の計算は簡単ではない。

　先に示した湿潤断熱減率は、高度に対する気温減率を与えるものであるが、断熱線図の縦軸は通常気圧である。そこで、気圧に対する気温の逓減率に式を変換すると以下の式が得られる。

　上記の式でもを乾燥空気の値として扱い定数化すると、、以下に示すような簡略式が得られる。

　ここで、それぞれの定数は、以下のような値となる。

　ただし、この式も気圧を少しずつ変化させながら、飽和混合比を逐次計算して、気圧の変化にしたがう気温を計算しなければならない。以下に、Stullの教科書に紹介されている方法で計算する手法を示す。なお、Stullの教科書では気圧の単位がkPAであるが、これを国内の一般的な単位であるhPaに変換した。

　計算の初期値の高度として、気圧1000 hPaを選び、その高度での気温を選択するが、ここでは20℃を選択した。これらの初期値を用いて、飽和混合比を計算するが、そのためには、その気圧と気温における飽和水蒸気圧を計算する必要がある。その計算には、（飽和水蒸気圧曲線を描く　(1)）で導いた、以下に示すクラウジウス・クラペイロンの式を用いる。

　得られた飽和水蒸気圧と気圧を用いて、以下の式から飽和混合比が計算できる。

　ここで、εは乾燥空気と水蒸気のモル質量の比の逆数となり、以下の値となる。

　これらの値を用いて、先に示した気温の気圧による変化量の微分式を差分式に置き換えて、気温の変化量を計算する。ここでは気圧を20 hPa刻みで減少させながら、以上の計算を繰り返し、水蒸気で飽和した空気塊の高度上昇に伴って気温の低下を計算する。

　エクセルを用いた計算は次回に示す。

(2011.4.7)