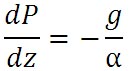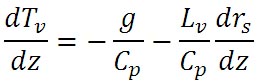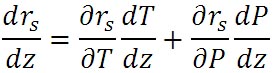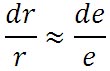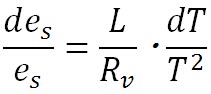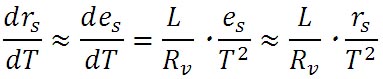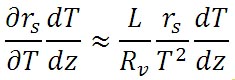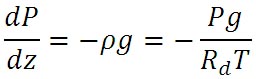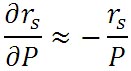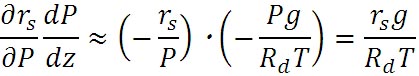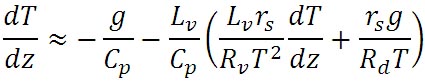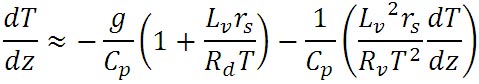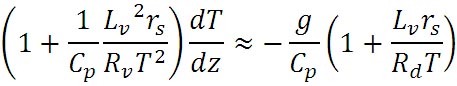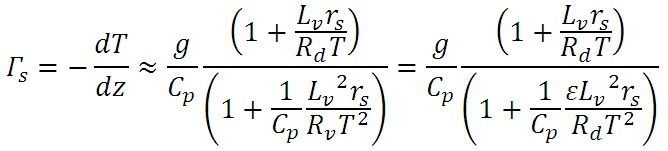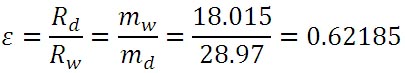湿潤断熱線図を描く (1)
空気塊が断熱的に上昇すると、その空気塊の温度は低下するが、その空気塊が水蒸気によって飽和しない場合には、空気塊の温度は乾燥断熱減率(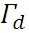 )にしたがって低下する。乾燥断熱減率は、(乾燥断熱線図を描く(1))で導いたように、 )にしたがって低下する。乾燥断熱減率は、(乾燥断熱線図を描く(1))で導いたように、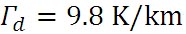 である。乾燥断熱減率は、英語でもそのままdry adiabatic lapse rateというが、「乾燥」という言葉を用いると、空気塊に水蒸気が含まれていないかのような印象を与えることから、不飽和断熱減率(unsaturated adiabatic lapse rate)という用語を使用することもある。 である。乾燥断熱減率は、英語でもそのままdry adiabatic lapse rateというが、「乾燥」という言葉を用いると、空気塊に水蒸気が含まれていないかのような印象を与えることから、不飽和断熱減率(unsaturated adiabatic lapse rate)という用語を使用することもある。
空気塊が水蒸気によって飽和した後に空気塊がさらに高度上昇すると、その空気塊の温度は湿潤断熱減率にしたがって低下する。湿潤断熱減率は、英語でmoist adiabatic lapse rateといわれてきた。ただ、この湿潤の意味は、単に空気中に水蒸気が含まれているということではなく、空気塊が水蒸気で飽和しているという意味であることから、飽和断熱減率(saturated-adiabatic lapse rate あるいは saturation adiabatic lapse rate)の用語の方がよく用いられるようになった。湿潤断熱減率を示す記号も、飽和を意味する s を添え字とした(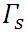 )が用いられる。 )が用いられる。
湿潤(飽和)断熱減率の計算式を導く出発点は、乾燥(不飽和)断熱減率のときと同様に熱力学第1法則(エネルギー保存の法則)である。その式は、やはり(乾燥断熱線図を描く (1))で紹介したとおり、仮温度を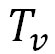 とすると、以下の式で表される。 とすると、以下の式で表される。
ここで、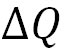 は、外部から空気塊に与えられる熱量であるが、断熱変化では、この項は0となる。 は、外部から空気塊に与えられる熱量であるが、断熱変化では、この項は0となる。
空気塊の内部で水蒸気の凝結が生じている場合には、空気塊の飽和混合比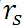 の減少分に応じた水蒸気が凝結していることになる。 ここで、 の減少分に応じた水蒸気が凝結していることになる。 ここで、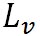 を、水蒸気から水の状態へと相変化する際に放出される潜熱、 を、水蒸気から水の状態へと相変化する際に放出される潜熱、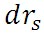 は飽和混合比の変化量で、空気塊の単位質量あたり凝結した水の質量となる。すると、 は飽和混合比の変化量で、空気塊の単位質量あたり凝結した水の質量となる。すると、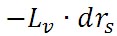 に相当する潜熱が放出される。マイナス符号が付いているのは、飽和混合比が減少するときに、潜熱が放出されるからである。しったがって、この場合のエネルギー保存の法則は以下の式で表される。 に相当する潜熱が放出される。マイナス符号が付いているのは、飽和混合比が減少するときに、潜熱が放出されるからである。しったがって、この場合のエネルギー保存の法則は以下の式で表される。
湿潤断熱変化をする場合は、放出される潜熱によって、乾燥断熱減率による気温低下と比べて、気温の低下割合が少なくなる。
次に、この式の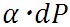 を、以下に示す静水圧平衡の式を用いて消去する。 を、以下に示す静水圧平衡の式を用いて消去する。
すると、以下のような式が得られる。
この式の右辺の第2項の微分式が表す水の凝結量の高度による変化を、気温による変化の項と気圧による変化の項とに分解すると、次の式が得られる。
この先の式の変形には、各種の近似関係を利用することになるが、まず、混合比の変化率と水蒸気圧の変化率とはほぼ等しいとする近似を利用する。すなわち、以下の近似式が成立する。
ここで、(飽和水蒸気圧曲線を描く (1))で、クラウジウス・クラペイロンの式を導く際に導入した微分方程式を利用する。それは、
である。この式と、その前に示した近似式とをを利用すると、
が得られる。したがって、水の凝結量の高度による変化を表す式の右辺第1項は以下のような式に変形できる。
続いて、水の凝結量の高度による変化を表す式の右辺第2項を、以下に示す理想気体の状態方程式と静水圧平衡の式を用いて整理する。、
すると、以下に示す式が得られる。
ここで、さらに以下に示す近似式を用いる。
その結果、水の凝結量の高度による変化を表す式の右辺第2項は、以下のようになる。
以上の結果をまとめると、高度による気温の変化を示す式として、以下の近似式が得られる。
この式の、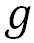 の含まれる項をまとめて整理すると、以下の式が得られる。 の含まれる項をまとめて整理すると、以下の式が得られる。
さらに、dT/dzの項をまとめると、以下の式が得られる。
湿潤断熱減率とは、高度上昇にともなる気温の低下率を示すものであるから、以下の式が得られる。
ここで、εは、乾燥空気の比気体定数と水蒸気の比気体定数との比である。式中、水蒸気を表す添え字の v と、水を表す添え字の w が混在しているが、両者の値は同一である。
計算の途中から、いくつかの近似式を用いて式の変形をしているが、ここで得られた計算式の精度はかなり高いとされている。自然大気中には凝結核が豊富に存在するため、空気塊が上昇したり加工したりする際に、たとえ過飽和状態が生じたとしても、通常過飽和度は1%を超えることは稀とされる。
水蒸気で飽和した空気塊が断熱上昇すると水や氷晶の凝結生成物が生じるが、それが空気塊内にとどまれば、空気塊が加工したときに凝結生成物が再び蒸発し、可逆的な温度変化をするが、この過程が湿潤断熱過程である。一方、凝結生成物が生じてすぐに空気塊の外に排出されてしまうと、元に戻る際に可逆的な温度変化をせず、このような過程を偽断熱過程(pseudo-adiabatic)という。偽断熱過程の式は、湿潤断熱過程とわずかに異なるが、通常はその差を無視する。
(2011.4.5)
| 
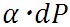 を、以下に示す静水圧平衡の式を用いて消去する。
を、以下に示す静水圧平衡の式を用いて消去する。