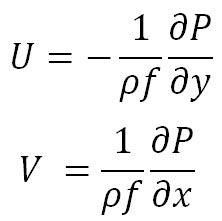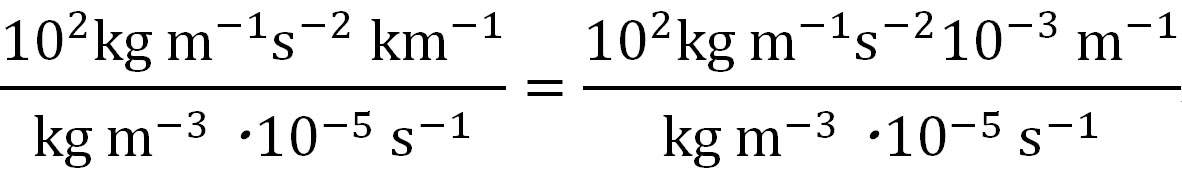地衡風 (3)
これまでに、自由大気中に気圧傾度が存在するときに吹く地衡風の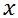 方向(東向き)の風速 方向(東向き)の風速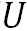 と と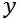 方向(北向き)の風速 方向(北向き)の風速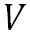 を表す以下に示すような式を求めた。 を表す以下に示すような式を求めた。
これらの式には、気圧傾度のほかに、空気の密度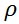 とコリオリ・パラメータ とコリオリ・パラメータ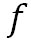 が含まれている。空気の密度は高度によって変化するため、空気密度の高度変化を計算する近似式と、その計算値と1976年米国標準大気モデルの空気の密度の比較を前回行った。 が含まれている。空気の密度は高度によって変化するため、空気密度の高度変化を計算する近似式と、その計算値と1976年米国標準大気モデルの空気の密度の比較を前回行った。
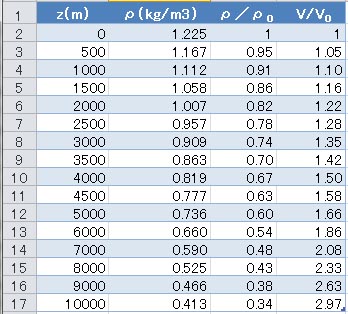
地衡風の風速の計算式で、空気密度は分母にあるため、上空での地衡風速を計算する際に空気密度の値として海面の値を使用すると、地衡風速を過小評価することになる。空気密度の値を変化させた地衡風速の計算結果と、上空においても海面における空気密度を使用して地衡風速を計算した場合に得られる値との比を計算した結果を以下の表に示す。
上に示した表では、左側の列から順に、メートルを単位とした高度、その高度における空気密度、各高度における空気密度と海面における空気密度のとの比が示されている。そして、一番右側の列は空気密度比の逆数で、この値は、空気密度の値を高度補正した場合と海面の値を用いた場合の地衡風速の比となる。当然のことながら、空気密度を補正して計算した地衡風速と、海面の空気密度値をそのまま用いて計算した地衡風速の比は、上空に行くにしたがって増加する。高度5000 mでその差は約1.7倍、7000 mで約2倍、10000 mでは、その差は約3倍に拡大している。
日本付近の地衡風速を考えるとき、緯度33度16分(33.667度)の地点におけるコリオリ・パラメータは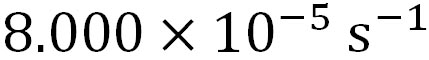 という切りの良い数字となる。そこで、この値を、しばらくの間コリオリ・パラメータとして用いることにする。ちなみに、この緯度の地点には佐賀県伊万里市のアメダス観測所がある。 という切りの良い数字となる。そこで、この値を、しばらくの間コリオリ・パラメータとして用いることにする。ちなみに、この緯度の地点には佐賀県伊万里市のアメダス観測所がある。
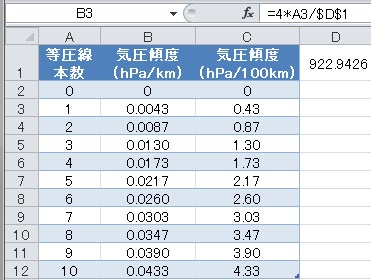
地上天気図には、4 hPa おきに等圧線が描かれている。ここで、経度10度の間に何本の等圧線が描かれているかで、気圧傾度の値を求めることにする。地球の半径を6353.766 kmとすると、緯度33度16分に沿った周長は33225.93 km、経度10度で切り取られる長さは922.9426 kmとなる。この値を用いて、経度10度の間にある等圧線本数と、その時の気圧傾度の関係を求めた結果を以下の表に示す。
D1セルに、緯度33度16分に沿った経度10度の円周長さの計算結果が示されている。列Aに等圧線本数、列Bに気圧傾度を hPa/kmの単位で求めた結果を、列Cには、列Bの値を100倍して、hPa/100km の痰とした気圧傾度を示した。数式バーには、B3セルの内容が表示されている。
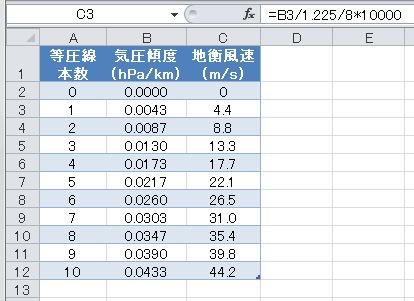
この表の列Cを地衡風速としたものを下の表に示す。地衡風速の計算式は、気圧傾度を空気密度とコリオリ・パラメーターで除しただけであるから、式は単純だが単位の換算には注意する必要がある。
気圧傾度の単位を分解すると、
となることから、地衡風の計算式の次元と指数の計算は次のようになる。
上の式を整理すると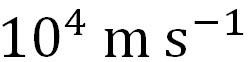 が残ることから、104の補正項が残る。上のエクセルのシートの数式バーにはC3セルに代入されている計算式が示されているが、*10000があるのは、そのためである。 が残ることから、104の補正項が残る。上のエクセルのシートの数式バーにはC3セルに代入されている計算式が示されているが、*10000があるのは、そのためである。
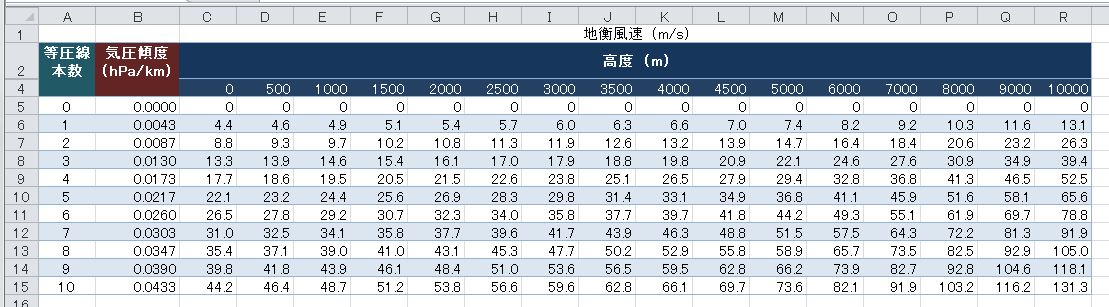
上に示した計算結果と、最初に掲げた高度上昇による速度の増加を示す表を組み合わせて、等圧線の本数と地衡風速との関係を各高度別に計算した結果を以下の表に示す。
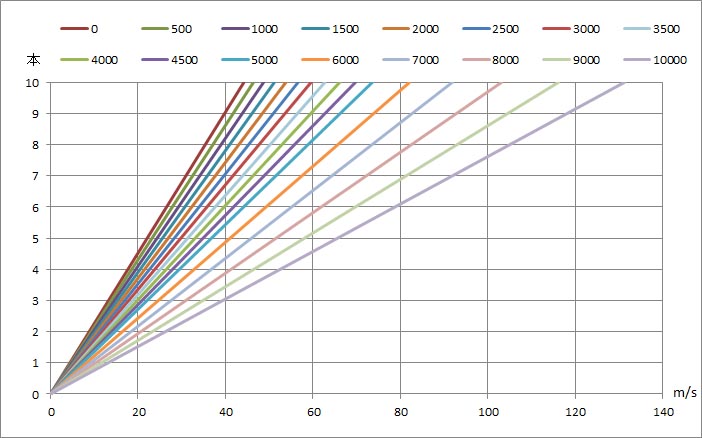
上に示した計算結果をグラフにすると、以下のようになる。
経度10度の間に4本の等圧線があると、地上では17.7 m/s、高度5000 mでは29.4 m/s、高度1万 mでは52.5 m/sの地衡風が吹くことになる。計算上は、同じ気圧傾度でも、高度1万 mの地衡風は地上の地衡風の風速の約3倍の風速となる。ただし、地上では地表との摩擦や障害物の影響でここで計算した風速よりは小さくなり、通常地衡風の計算の対象外である。
(2011.11.9)
|