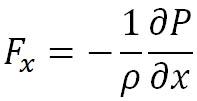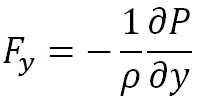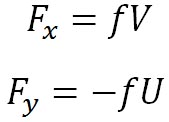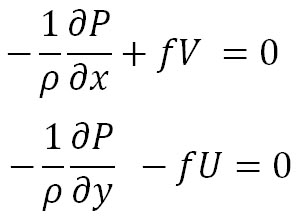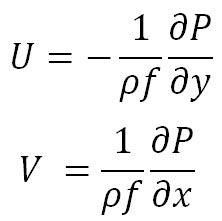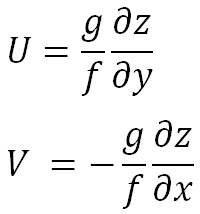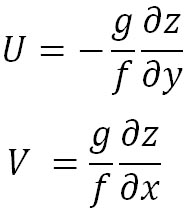地衡風 (1)
気圧傾度力とコリオリ力が釣り合った状態の時に吹く風を地衡風(Geostrophic Wind)という。等圧線の曲率が小さく(等圧線が直線に近い)、地形や地表との摩擦の影響が無視できる高度1km程度以上の自由大気中で吹いている風は、ほぼ地衡風となっている。この地衡風は、等圧線に平行に吹いている。
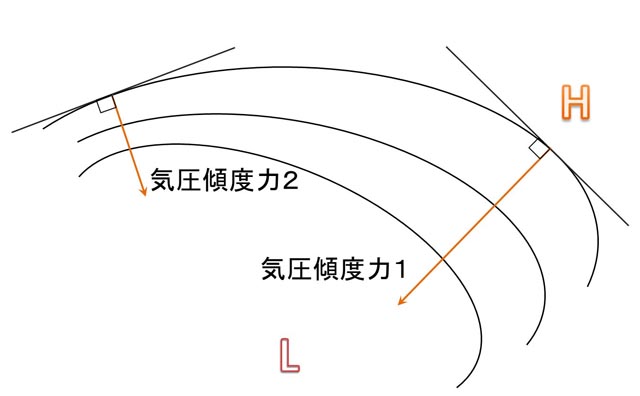
ここで、気象学で考える気圧傾度力は、水平方向に圧力勾配があるときに作用する力である。気圧傾度力は、以下の図に示すよう様に、気圧の高い方から低い方に向けて、常に等圧線に直角方向に作用する。
気圧傾度力が存在すると、風が吹き始め、すでに吹いている風を加速したり減速したりすることはあるが、風が吹いていることによって気圧傾度力が生じたり、気圧傾度力の大きさが変化したりすることはない。気圧傾度力は、気圧の傾度によってのみ作用する力である。
等圧線の間隔が狭い場所では気圧傾度力は大きく、等圧線の間隔が広い場所では気圧傾度力は小さくなる。したがって、上の図で、気圧傾度力1より気圧傾度力2の方が大きい。
気圧傾度力は、風が全くないところに風を生じさせることができる。一方、コリオリの力や遠心力は、吹いている風の方向を変化させる作用はあるが、風のないところに風を生じさせることのできる力ではない。
気圧傾度力は、気圧の勾配の方向に作用するが、その力を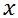 方向と 方向と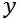 方向に分解して考える。 方向に分解して考える。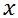 方向の気圧の勾配を 方向の気圧の勾配を
とすると、単位質量の大気に作用する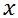 方向の気圧傾度力は 方向の気圧傾度力は
となる。ここで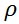 は空気の密度である。マイナスの符号は、気圧傾度力が気圧の高い方向から低い方向に向けて働くことから付けられている。同じく、 は空気の密度である。マイナスの符号は、気圧傾度力が気圧の高い方向から低い方向に向けて働くことから付けられている。同じく、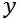 方向の気圧の勾配を 方向の気圧の勾配を
とすると、単位質量の大気に作用する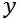 方向の気圧傾度力は 方向の気圧傾度力は
となる。
地衡風は、この気圧傾度力とコリオリの力とが釣り合った状態の時に吹く風である。コリオリの力は、前回示したように、
であるから、気圧傾度力とコリオリの力とが釣り合った状態は、以下の式で表される。
上の式を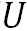 と と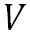 について解くと、 について解くと、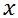 方向と 方向と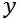 方向の地衡風の風速を表す以下の式が得られる。 方向の地衡風の風速を表す以下の式が得られる。
実際の地衡風の風速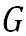 は、 は、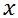 方向と 方向と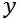 方向の地衡風の風速にピタゴラスの定理を用いて、以下の式で得られる。 方向の地衡風の風速にピタゴラスの定理を用いて、以下の式で得られる。
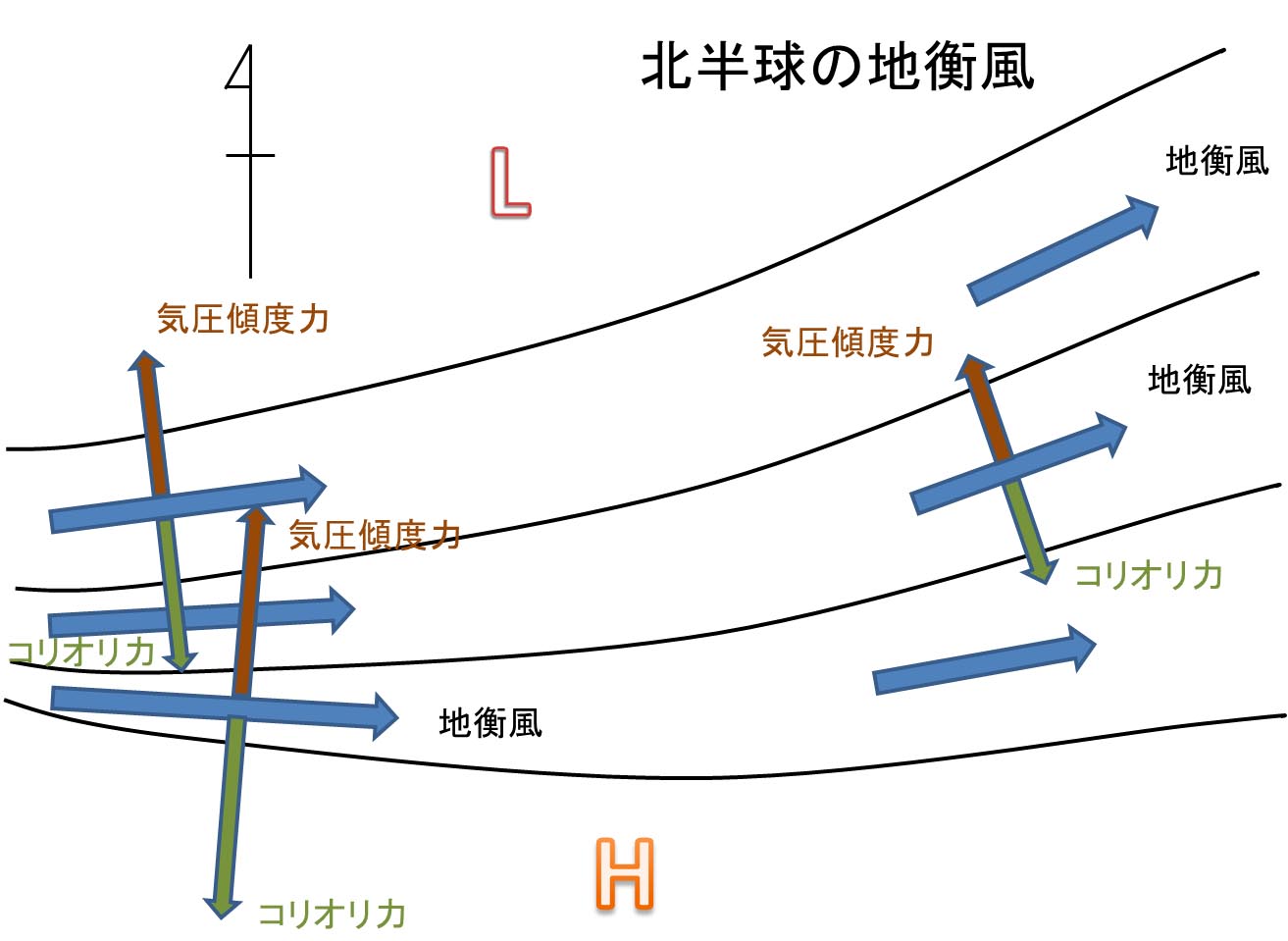
地衡風は、気圧傾度力の大きいところで強いことから、等圧線の間隔が狭い部分で強い風が吹き、等圧線の間隔が広い部分で風は弱い。また北半球における風向は、低気圧を左手に、高気圧を右手に見る方向となる。その状況を模式的に示したものが、以下に示す図である。
ところで、高層天気図は、通常等圧面天気図が用いられることから、地衡風の計算式も、距離に対する気圧変化を用いる式より、距離に対する高度変化を用いる式の方が実用的である。その式の変換を行うには、静力学平衡の式を用いる。その式は以下に示すものである。
この式を、気圧差の値から求めた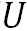 と と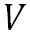 を与える式の を与える式の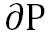 を消去すると、以下の式が得られる。 を消去すると、以下の式が得られる。
上に示した式は、以前の式と符号が異なっている。地衡風の風向は、北半球では低気圧を左手に見る方向に吹くことには変わりないので、その関係から、式の符号は気圧差の値から求めた式のものと同じとなり、以下の式が求める式である。
今回も、エクセルの出番はなかった。
(2011.10.18)
|