シミュレーションを行うには、乱数の発生は基本テクニックとなる。エクセルでは擬似乱数を発生させるシート関数にがある。擬似乱数としたのは、周期性がある簡易な乱数だからである。ただ、シミュレーションの目的では擬似乱数でも傾向を確かめる上では十分使える。

　この関数の使用法は簡単で、任意のセルに=RAND()と書き込めば、0から1の間でほぼ均等に分布して発生する擬似乱数を１個取りだせる。ただ、シミュレーションで使用するとなると、ワークシートでの作業は大変なので、マクロで処理するのが現実的である。

　エクセルのマクロで利用する擬似乱数はシート関数とは異なりRnd(number)関数を使用する。引数のnumberには、任意の有効な数式を指定するが、負の値となる数値や数式を指定すると、0以上1未満の単一の（同じ値の）数値を返す。従って、シミュレーションを行う上での乱数としては使えない。引数に正の数値や数式を指定すると、次々に新たな乱数が発生するので、シミュレーションを行う上で普通の使い方ができる。引数に0を指定すると、直前に生成した乱数を返す。これも、シミュレーションの普通の使い方では用いられない。引数欄を空白にしておくと、正の数値を指定したときと同じように、次々と新たな乱数を発生する。このため、通常は引数欄を空白にして使用する。

　以下のプログラムを書き１０００個の擬似乱数を発生させる実験を１０回繰り返し、発生した1000個の擬似乱数の平均と標準偏差を求めた。

Dim i
For i=1 to 1000
Cells(i,1)=Rnd(1)
Next
End Sub

また、以下のプログラムも１０回実行して、発生した1000個の擬似乱数の平均と標準偏差を求めた。

Dim i
For i=1 to 1000
Cells(i,1)=Rnd()
Next
End Sub

　引数に１を指定したとき、1000個の擬似乱数の平均値10個の平均は0.500、10個の標準偏差の平均値は0.290だった。同様に引数を空白にしたときの値は平均が0.502、標準偏差0.289だった。これらの理論値は0.5と0.289であるから（分散が1/12）、乱数の数を多くすれば、かなり良い発生分布をしている。

　乱数の初期値を変化させるためにはRandomize(number)ステートメントを使用する。numberは任意の数値、数式を指定するのだが、引数は省略可能で、省略した場合はシステムタイマーから取得された値が使用される。通常は引数を省略する。Randimizeは、Rndの前に記述すればどこに置いてもよい。

　自然現象の発生をシミュレートするときは、発生分布を区間一様ではなく、正規分布すると仮定することの方が多い。したがって、生起確率が正規分布する乱数が必要となる。エクセルで正規乱数を発生させるには、 正規分布の累積分布関数の逆関数値を返すNORM.INV関数を用いる。以前はNORMINV関数を用いていたが、NORM.INV関数の方が精度が高いという。

　NORM.INV関数は３つの引数があり、NORM.INV（確率、平均、標準偏差）という形式で利用する。これら3つの引数は必ず指定する必要がある。引数に数値以外の値を指定すると、エラー値#VALUE!が返される。引数に指定した確率の値が 0 以下あるいは 1 以上である場合は、エラー値#VALUE!が返される。同じく、引数に指定した標準偏差の値が 0 以下の場合は、エラー値#VALUE!が返される。平均 = 0 かつ標準偏差 = 1 である場合、標準正規分布関数の逆関数の値が返されるが、それには、標準正規分布関数の逆関数の値を返す専用の関数NORM.S.INV 関数が利用できる。

　計算の原理は、正規分布の累積分布関数の数表を検索するもので、以前の検索方法を改善したものがNORM.INV関数である。確率の値が指定される、NORM.DIST(x、平均、標準偏差,TRUE)=確率　となるxが検索される。したがってNORM.S.INV 関数の精度はNORM.DIST関数の精度に依存するが、NORM.DIST関数の精度も以前のNORMDIST関数の精度より向上しているという。

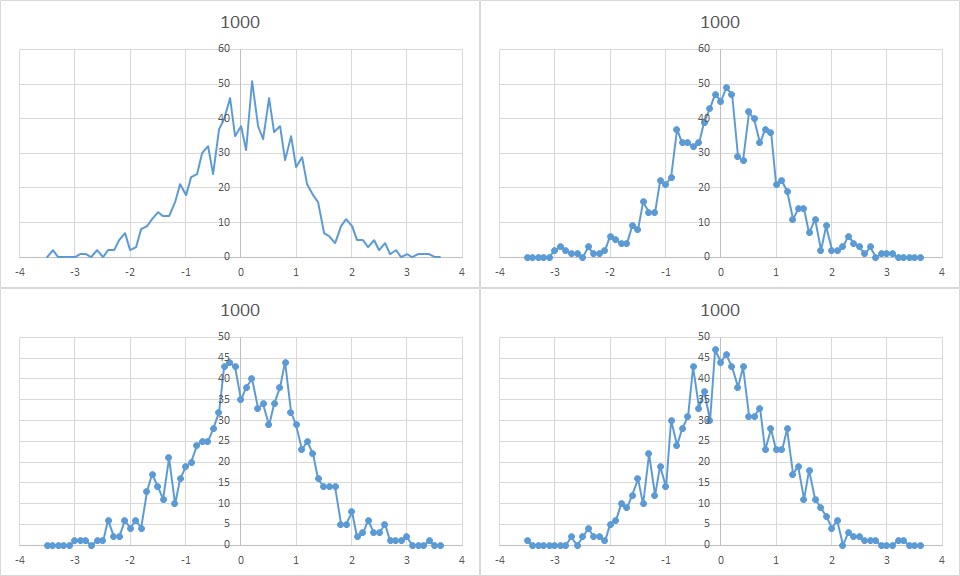
　実際に1000個の正規乱数を発生させた実験を20回行ったところ、NORMINV関数を用いると、平均値が0.0126、NORM.INV関数を用いると平均値が-0.00095となり、平均値に関してはNORM.INV関数の成績がよかった。 NORM.INV 関数を用いて、平均0.0、標準偏差1.0の正規乱数を1000個発生させた結果の4回分のヒストグラムを示す。

　1000個程度の乱数を発生させると、正規分布を感じさせる分布になってくる。

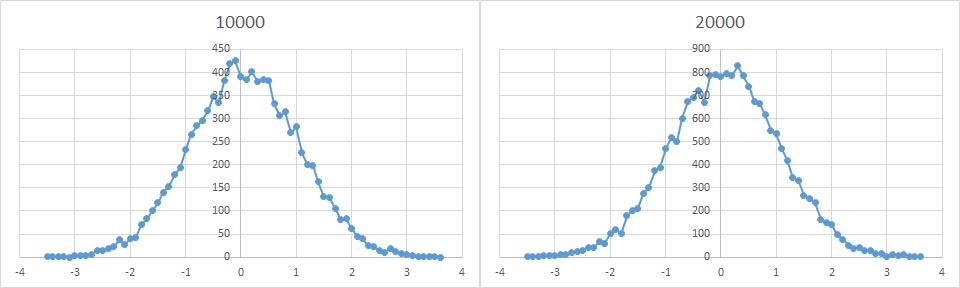
　さらに多くの乱数を発生させた場合の乱数の分布として、10000個及び20000個の乱数を発生させた時のヒストグラムを示す。

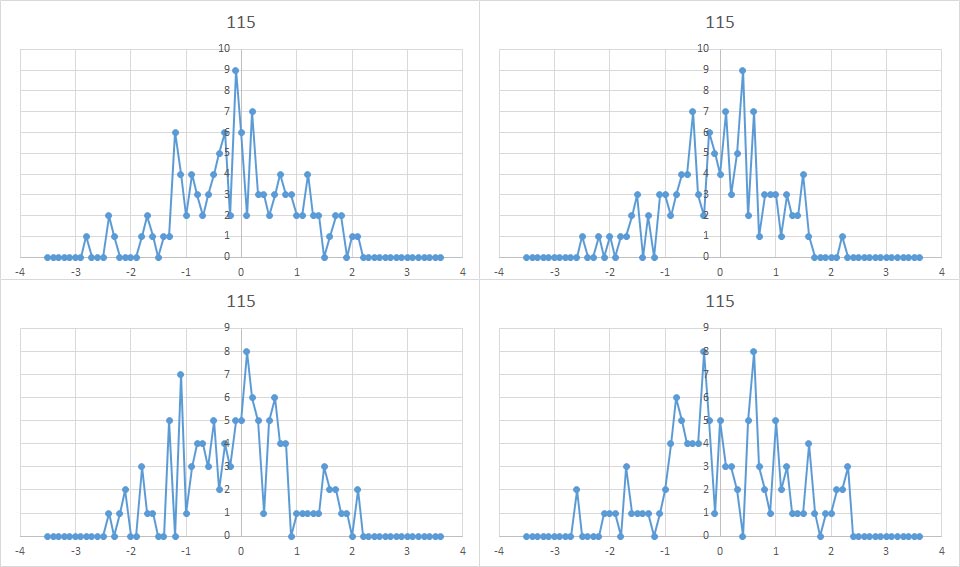
　この100年間の気温変動をシミュレートする場合には、もっと少ない乱数で処理することになる。115個発生させた場合の結果を下に示す。

　100個程度の正規乱数では、中央部がへこんでいる場合も結構出現するようだ。

　ところで、マクロを使用する場合、NORM.DISTアプリケーション関数に はなく、NORMINV関数を用いなければならないようである。そこで、以下のようなプログラムをマクロの記録機能を利用して作成した。

Sub Macro1()

Dim i
Randomize

For i = 1 To 10000
Cells(i, 1) = Application.NormInv(Rnd(), 0, 1)

Next

Application.Run "ATPVBAEN.XLAM!Histogram", ActiveSheet.Range("$A$1:$A$10000" _
), ActiveSheet.Range("$E$1"), ActiveSheet.Range("$C$1:$C$72"), False, False _
, False, False
ActiveWindow.SmallScroll Down:=-12
Range("E2:F73").Select
ActiveWindow.SmallScroll Down:=-60
ActiveSheet.Shapes.AddChart2(240, xlXYScatterLines).Select
ActiveChart.SetSourceData Source:=Range("Sheet1!$E$2:$F$73")
ActiveChart.ChartTitle.Select
ActiveChart.ChartTitle.Text = "10000"
Selection.Format.TextFrame2.TextRange.Characters.Text = "10000"
With Selection.Format.TextFrame2.TextRange.Characters(1, 5).ParagraphFormat
.TextDirection = msoTextDirectionLeftToRight
.Alignment = msoAlignCenter
End With
With Selection.Format.TextFrame2.TextRange.Characters(1, 5).Font
.BaselineOffset = 0
.Bold = msoFalse
.NameComplexScript = "+mn-cs"
.NameFarEast = "+mn-ea"
.Fill.Visible = msoTrue
.Fill.ForeColor.RGB = RGB(89, 89, 89)
.Fill.Transparency = 0
.Fill.Solid
.Size = 14
.Italic = msoFalse
.Kerning = 12
.Name = "+mn-lt"
.UnderlineStyle = msoNoUnderline
.Spacing = 0
.Strike = msoNoStrike
End With

End Sub

　4回実行して、正規乱数を10000個発生させた分布のグラフを並べて示す。

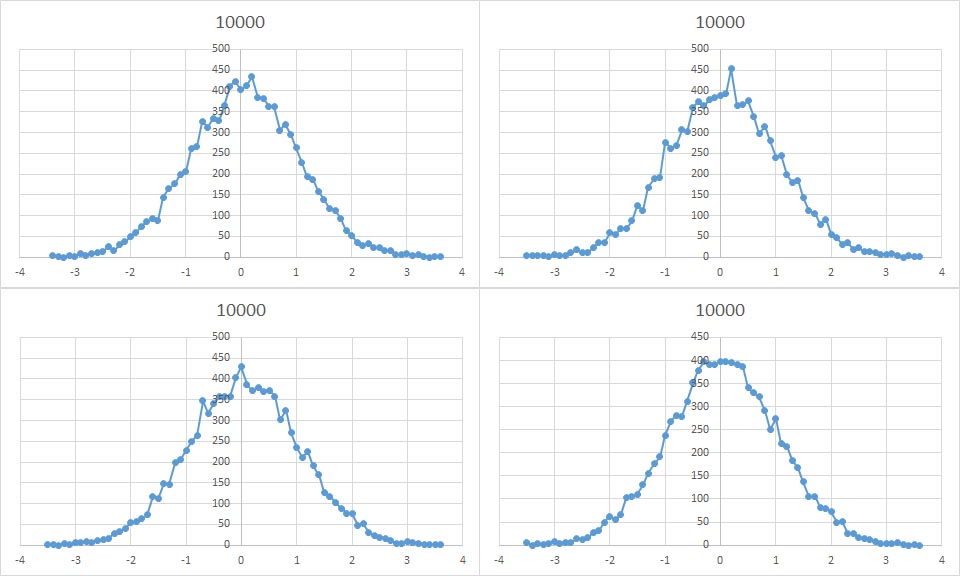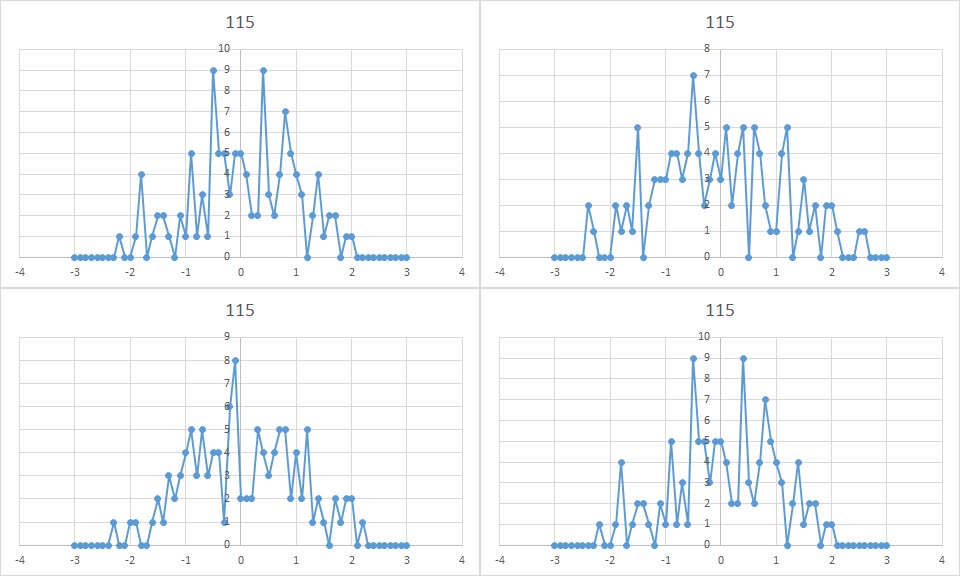
　上に示したプログラムを置換機能を用いて10000を115に、Characters(1, 5)をCharacters(1, 3)にそれぞれ置換すると、115個の正規乱数を発生させて、その分布のグラフを作成できる。4回実行した結果のグラフを下に示す。

　これで、簡単なシミュレーションを行う準備が整ったことになる。

(2014.4.17)