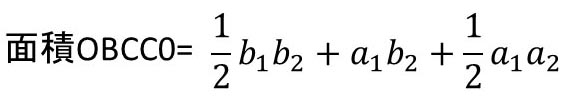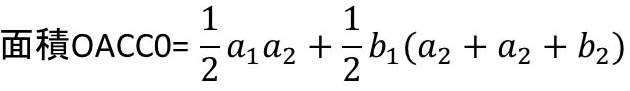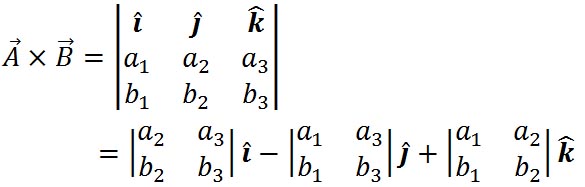ベクトルのクロス積 (1)
ベクトルの掛け算(積)にはドット積とクロス積の2種類があり、その内のドット積については前回説明した。今回はクロス積について説明する
3次元空間のベクトル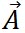 と と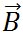 のクロス積は のクロス積は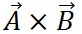 と書き、通常AクロスB(エー・クロス・ビー)と読む。 と書き、通常AクロスB(エー・クロス・ビー)と読む。
クロス積は、方向と大きさを持ったベクトルで、その大きさは、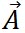 と と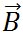 を隣り合う2辺とする平行四辺形の面積となる。そして、その方向は、右ねじの法則あるいは右手の法則と呼ばれるルールにしたがう。すなわち を隣り合う2辺とする平行四辺形の面積となる。そして、その方向は、右ねじの法則あるいは右手の法則と呼ばれるルールにしたがう。すなわち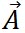 から から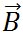 の方向に右ねじを回したとき、ねじが進む方向である。 の方向に右ねじを回したとき、ねじが進む方向である。
ここで、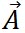 と と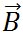 を隣り合う2辺とする平行四辺形の面積は、 を隣り合う2辺とする平行四辺形の面積は、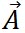 と と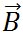 のなす角度をθとすると、 のなす角度をθとすると、
となる。これらの関係を図にすると、以下のようになる。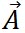 から から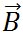 の方向に右ねじを回すと、右ねじは手前に浮き出してくる。すなわち、 の方向に右ねじを回すと、右ねじは手前に浮き出してくる。すなわち、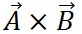 の方向は、平行四辺形の含まれる平面から垂直に手前に飛び出す方向となる。 の方向は、平行四辺形の含まれる平面から垂直に手前に飛び出す方向となる。
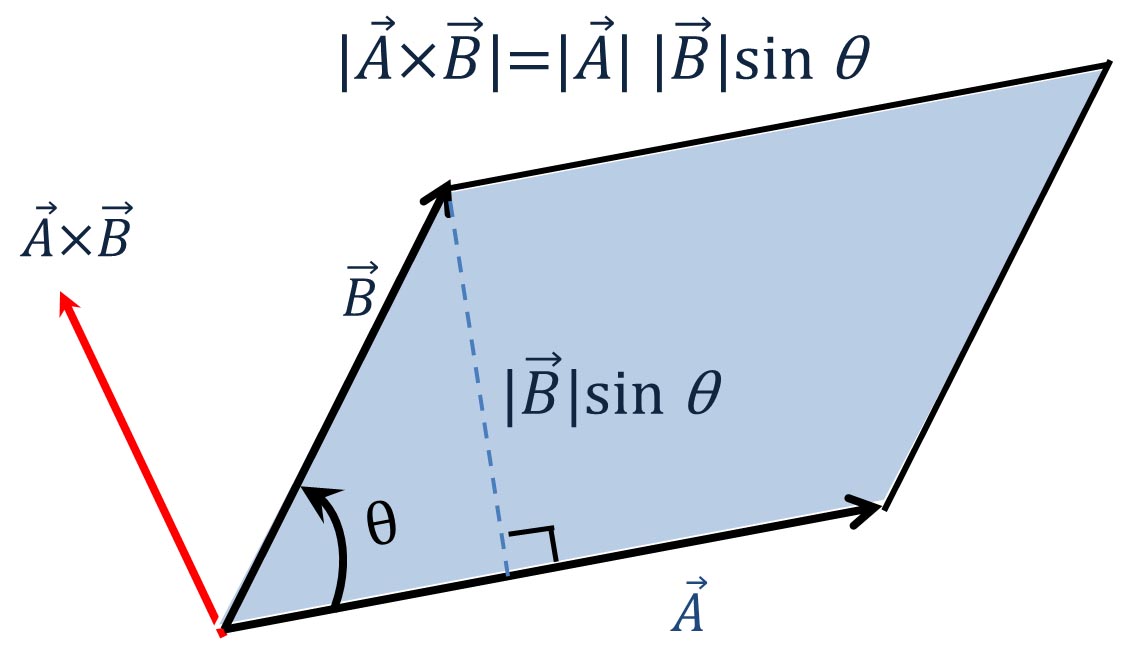
ここで、それぞれのベクトルの始点を座標の原点に移動し、ベクトルの終点の座標によってベクトルを表した場合に、この平行四辺形の面積がどのようになるかを考えてみよう。その大きさを、以下の図を用いて説明する。
ここで、求めるものは平行四辺形OBCAの面積である。平行四辺形OBCAの頂点Aの座標は
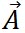 の終点の座標で の終点の座標で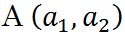 、頂点Bの座標は 、頂点Bの座標は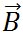 の終点の座標で の終点の座標で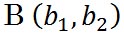 であるから、平行四辺形の頂点Cの座標は であるから、平行四辺形の頂点Cの座標は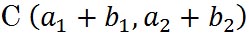 となる。 となる。
四角形OBCC0の面積は、三角形OBB0と台形B0BCC0の和で、
となる。一方、この四角形から平行四辺形部分を取り去ってできる四角形OACC0の面積は、三角形OAA0と台形ACC0A0の和で、
である。これらの結果から、求める平行四辺形の面積は以下のようになる。
この値は、以下に示すように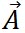 と と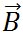 による行列式の値となっている。 による行列式の値となっている。
そして、この場合、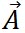 と と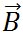 が が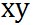 -平面上にあるとすると、 -平面上にあるとすると、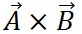 の方向は の方向は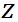 軸の方向を向いている。そして、その向きは右ねじの法則によれば、 軸の方向を向いている。そして、その向きは右ねじの法則によれば、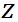 軸の正の方向である。したがって、 軸の正の方向である。したがって、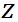 軸方向の単位ベクトルを 軸方向の単位ベクトルを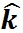 とすると、 とすると、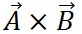 は、 は、
と表される。
同様に、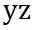 -平面上にある原点を始点とするベクトル -平面上にある原点を始点とするベクトル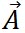 と と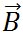 の終点の座標が の終点の座標が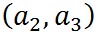 と と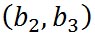 で表されるとき、 で表されるとき、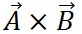 の方向は、右ねじの法則にしたがうと の方向は、右ねじの法則にしたがうと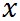 軸の正の方向を向いている。したがって、 軸の正の方向を向いている。したがって、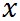 軸方向の単位ベクトルを 軸方向の単位ベクトルを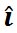 とすると、 とすると、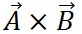 は、 は、
と表される。
一方、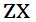 -平面上にある原点を始点とするベクトル -平面上にある原点を始点とするベクトル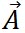 と と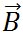 の終点の座標が の終点の座標が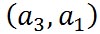 と と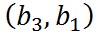 で表されるとき、 で表されるとき、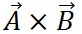 の方向は、右ねじの法則にしたがうと の方向は、右ねじの法則にしたがうと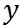 軸の負の方向を向いている。したがって、 軸の負の方向を向いている。したがって、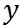 軸方向の単位ベクトルを 軸方向の単位ベクトルを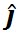 とすると、 とすると、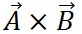 は、 は、
と表される。
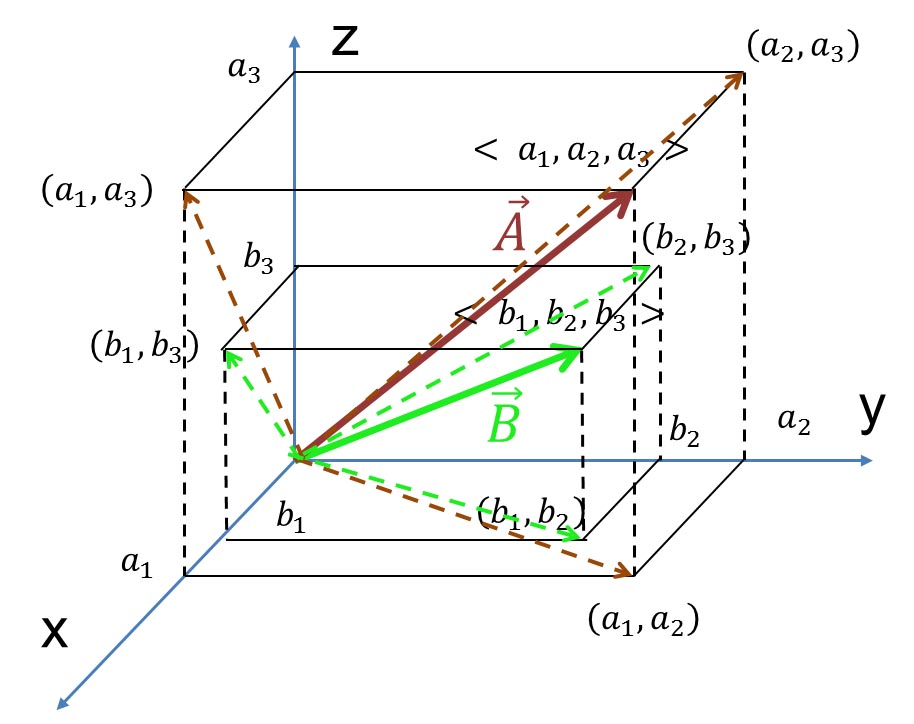
これらは、以下の図に示すように、3次元空間上のベクトルの各平面に射影した成分ベクトルのクロス積となっている。以下の図を見れば、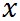 軸から 軸から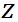 軸方向に右ねじを回すと、 軸方向に右ねじを回すと、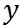 軸の負の方向にねじが進むことが分かるであろう。 軸の負の方向にねじが進むことが分かるであろう。
これらの3成分の和として、3次元のベクトルのクロス積は、以下の形式で表される。
(2011.8.8)
| 
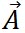 の終点の座標で
の終点の座標で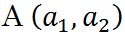 、頂点Bの座標は
、頂点Bの座標は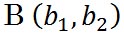 であるから、平行四辺形の頂点Cの座標は
であるから、平行四辺形の頂点Cの座標は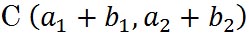 となる。
となる。