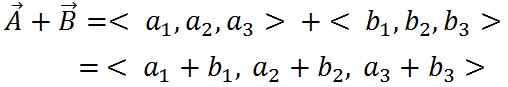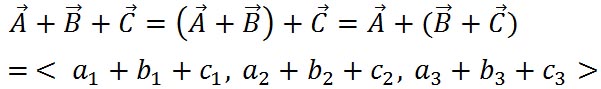ベクトルの加算
方向と大きさを持った量であるベクトルは、たとえば風向と風速で風の性質を表すのに使える。ところで、風向と風速の異なる2種類の風が合わさると、どのような風向と風速の風になるであろうか?ベクトルは足し算(加法・加算)と引き算(減法・減算)ができることから、このような問題にも応用できる。
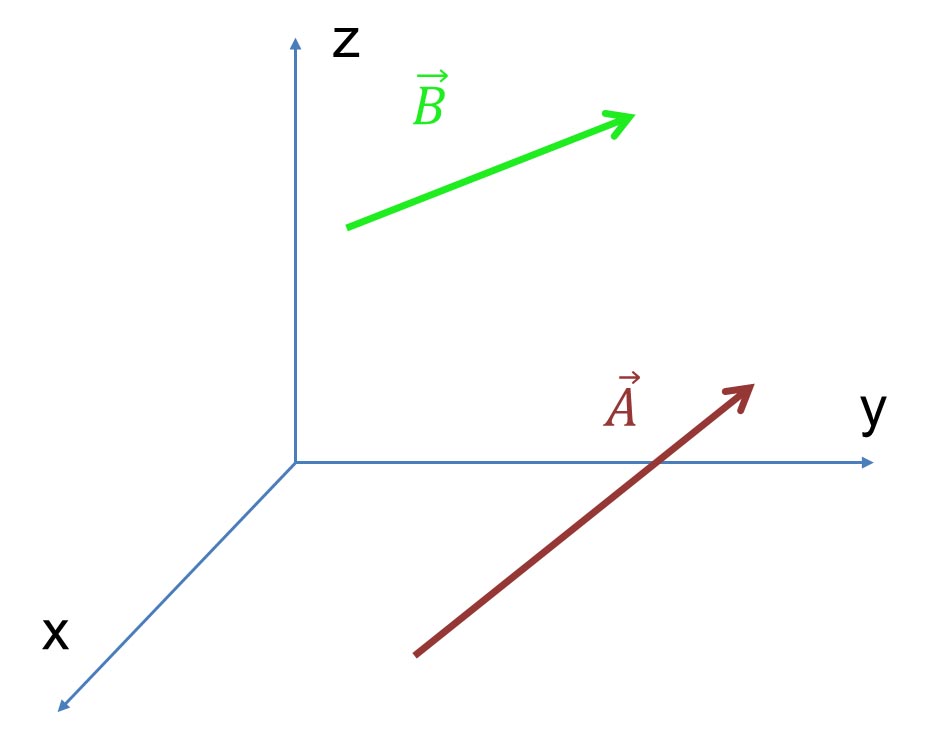
ベクトルの加算の例として、以下に示すベクトル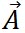 とベクトル とベクトル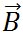 とを加え合わせてみよう。 とを加え合わせてみよう。
ベクトルは、方向と大きさが同じ量であれば、位置を移動しても同じベクトルである。そこで、それぞれのベクトルの始点を原点に移動してみる。
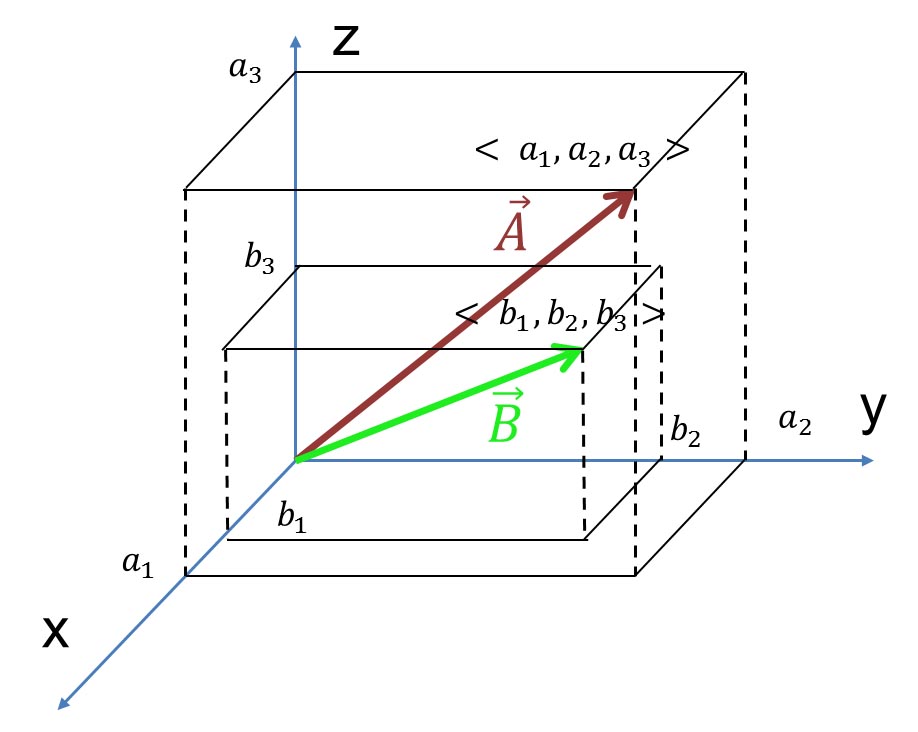
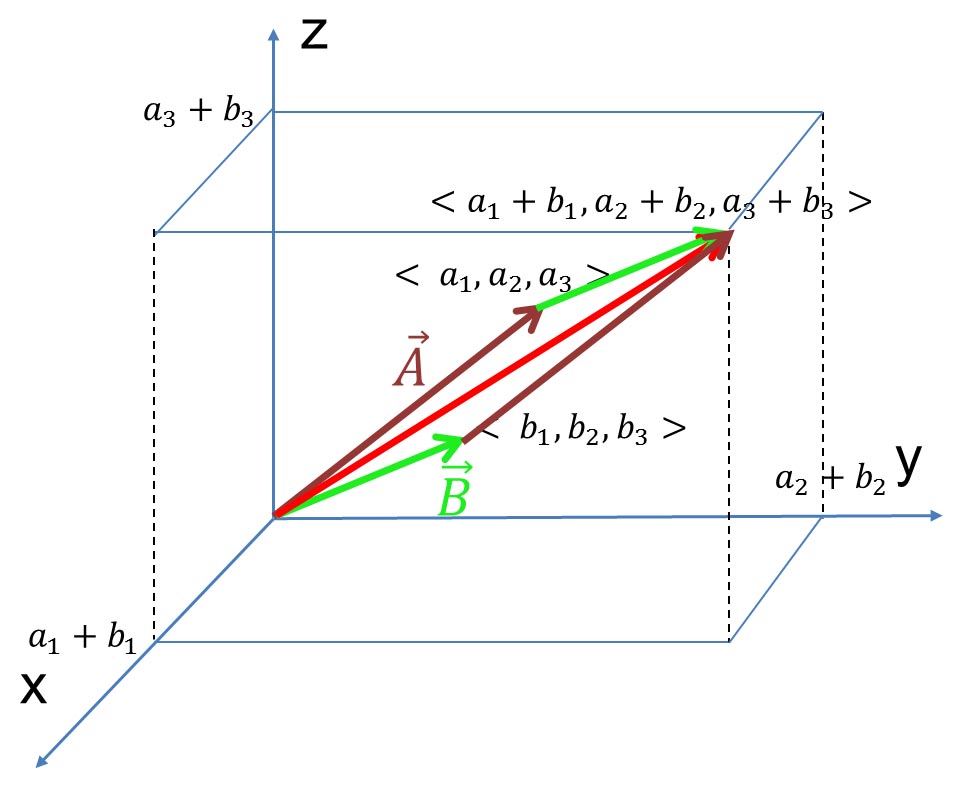
すると、ベクトル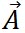 はその終点の座標 はその終点の座標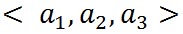 によって表され、ベクトル によって表され、ベクトル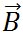 も、その終点の座標 も、その終点の座標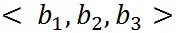 によって表すことができる。そして、これら二つのベクトルを加え合わせたベクトルは、次の式で示すように、これらの座標のそれぞれの要素を加え合わせることで表すことができる。 によって表すことができる。そして、これら二つのベクトルを加え合わせたベクトルは、次の式で示すように、これらの座標のそれぞれの要素を加え合わせることで表すことができる。
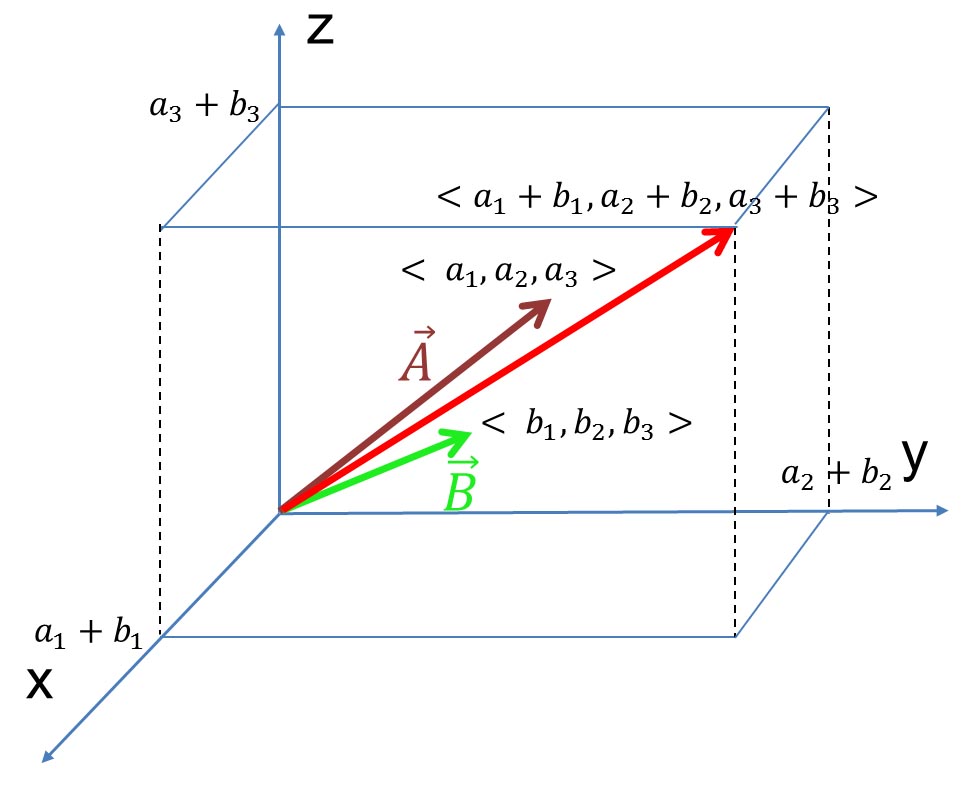
このベクトルを図で示すと、次の図のようになる。
同じ結果は、図形的にも求められる。ベクトルは平行移動しても同じベクトルなので、ベクトル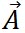 の始点をベクトル の始点をベクトル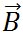 の終点まで移動し、ベクトル の終点まで移動し、ベクトル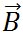 の始点とベクトル の始点とベクトル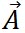 の終点を結べば、 の終点を結べば、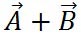 が得られる。同様に、 が得られる。同様に、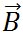 の始点を の始点を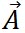 の終点まで移動することで、同様の結果が得られる。このことは、ベクトルの加算において、加算の順序を交換しても同じ結果が得られるという、交換法則が成り立つことを示している。 の終点まで移動することで、同様の結果が得られる。このことは、ベクトルの加算において、加算の順序を交換しても同じ結果が得られるという、交換法則が成り立つことを示している。
このようにして得られたベクトル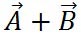 の長さは の長さは
となる。
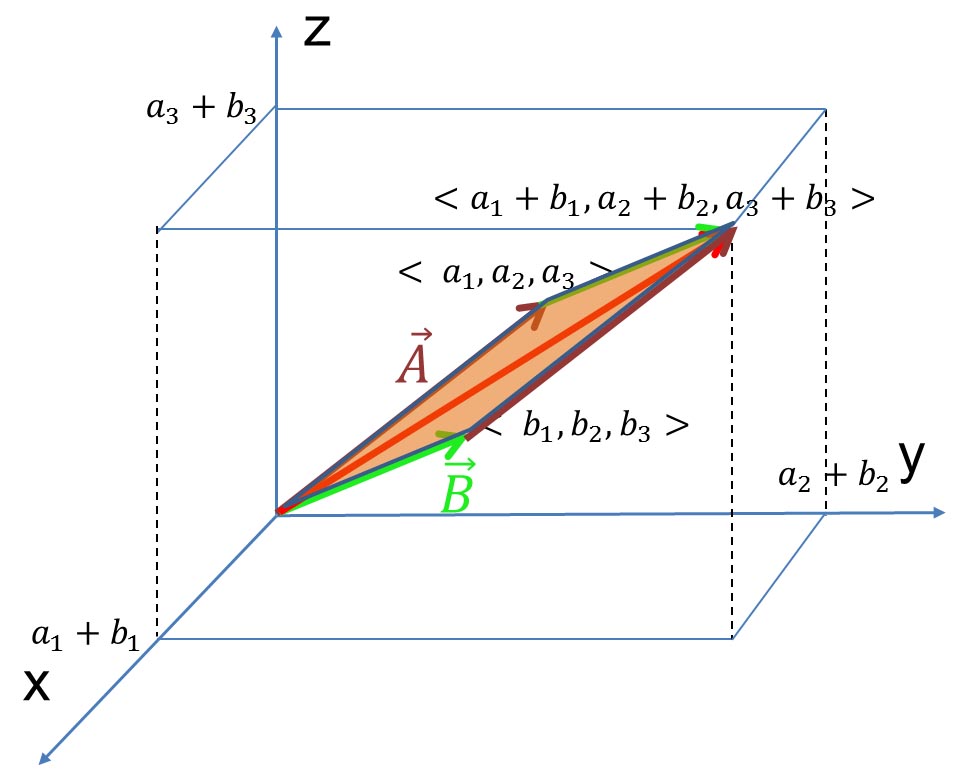
ここで、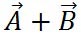 は、 は、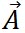 と と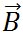 を含む平面上にある。これを、「 を含む平面上にある。これを、「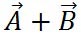 は、 は、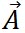 と と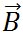 が張る平面上にある」、ということが多い。その平面を3次元的に示した図を以下に示す。 が張る平面上にある」、ということが多い。その平面を3次元的に示した図を以下に示す。
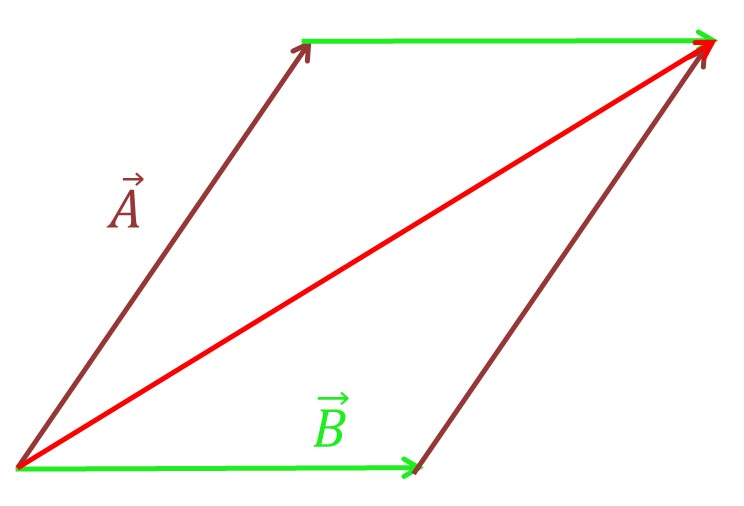
この平面上にあるベクトルを平面的に示した図を以下に示す。
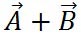 は、それぞれ は、それぞれ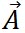 と と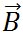 を隣り合う2辺とする平行四辺形の対角線となる。 を隣り合う2辺とする平行四辺形の対角線となる。
3つ以上のベクトルの加算も同様に計算できる。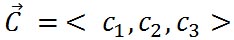 とすると、 とすると、
ここで、どちらの二つのベクトルを先に加え合わせても、結果は同じになる。すなわち、ベクトルの加算では、結合法則が成り立つ。
これらの3つのベクトルを加えて得られるベクトルの長さは、以下のようになる。
(2011.7.31)
|